Page 70 - 《摩擦学学报》2021年第1期

第 1 期 王美琪, 等: 基于SQPSO优化DELM的踏面磨耗测量模型 67

1.5 网络复杂度低，激活函数类型多样化等优点. 在随机
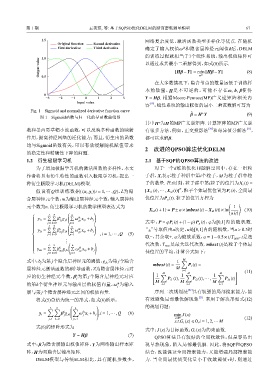
Original function Second derivative
First derivative Third derivative 确定了输入权值 ω 和隐含层神经元阈值 b后，DELM
ih
的训练过程就相当于1个线性系统，输出权值矩阵可
1.0
Output value 以通过求其最小二乘解得到，如式(8)所示. (8)

∥Hβ−Y∥ = min∥Hβ−Y∥
ω io
0.5
在大多数情况下，隐含节点的数量远低于训练样
本的数量， H是不可逆的，可能不存在ω, b, β使得
0
−3 −2 −1 0 1 2 3 Y = Hβ. 根据Moore-Penrose(MP)广义逆矩阵相关内
Input value
容 ，线性系统的输出权值的最小二乘范数解可写为
[19]

Fig. 1 Sigmoid and normalized derivative function curve
ˆ
+
β = H Y (9)
图 1 Sigmoid函数与归一化的导函数曲线图
其中 H 为 的MP广义逆矩阵. 计算矩阵的MP广义逆
+
H
数和墨西哥草帽小波函数，可以反映多种函数的映射 有很多方法，例如，正交投影法 和奇异值分解法 ，
[20]
[21]
作用，提高神经网络的泛化能力；而且，衍生出的函数 都可以求解 β.
均与Sigmoid函数有关，可以有效缓解随机赋值带来
2 改进的QPSO算法优化DELM
的稳定性和精确性下降的问题.
1.2 衍生极限学习机 2.1 基于SQP的QPSO算法的改进
为了增加极限学习机的激活函数的多样性，本文 对于一个 d维的优化问题解空间中，存在一组粒
作者将具有衍生特性的函数引入极限学习机，提出一 子群， X i表示粒子种群中第 i个粒子， M 为粒子群中粒
种衍生极限学习机(DELM)模型. 子的数量. 在 t时刻，粒子群中第 i粒子的位置为 X i (t) =
T
假设有 Q组训练数据 {(x i , y i )|i = 1,··· ,Q}，L为隐 [X i1 (t),··· , X id (t)] ，粒子个体最优位置为 P i (t)，全局最
含层神经元个数，m为输出层神经元个数，输入层神经 优位置为 P g (t). 粒子的位置方程为
元个数为n. 衍生极限学习机的数学模型表达式为 ( 1 )
X id (t +1) = P±α×|mbest (t)− X id (t)|×ln (10)
( ) u(t)

L ∑ Z ∑ n ∑
 k ih
 y 1i =

jp
1j
 β g jk ω x ip +b j
 式中： ，
 j=1 k=0 p=1 P = φP i (t)+(1−φ) P g (t) φ为[0,1]内的随机数.

 ( )

 L ∑ Z ∑ n ∑
 “ u决定， u是[0,1]内的随机数，当 u > 0.5时
ih
 y 2i = β g jk ω x ip +b j ±”号取值由

k

 2j jp
j=1 k=0 p=1 ,i = 1,··· ,Q (5)

 α为缩放系数， α = 1−0.5×t/T max t ， 是迭
 . 取−，其余取+.

 .


 . ( )
 代次数， mbest (t)是粒子个体最
 T max 是最大迭代次数.
 L ∑ Z ∑ n ∑
 k ih
 y mi =

jp
mj
 β g jk ω x ip +b j 佳位置的平均，计算公式如下：
j=1 k=0 p=1
式中：b 为第 j个隐含层神经元的阈值， g jk 为第 j个隐含 1 M ∑
j
mbest (t) = P i (t) =
层神经元激活函数的k阶导函数，Z为隐含层神经元对 M
 i=1  (11)
应的衍生神经元个数， β 为第 j个隐含层神经元对应  1 M ∑ 1 M ∑ 1 M ∑  
k

j   P i1 (t), P i2 (t),··· , P id (t)  
  M M M  
的第k个衍生神经元与输出层的权值向量， ω 为输入 i=1 i=1 i=1
ih
j
[22]
层与第 j个隐含层神经元之间的权值向量. 序列二次规划法 具有较强的局部搜索能力，能
[23]
将式(5)总结为统一的形式，如式(6)所示： 有效避免局部最优解现象 . 常用于解决形如式(12)
  的规划问题：
Z n
L ∑∑
∑  

ih
k

,
y i = β g jk     ω x i +b j i = 1,··· ,Q (6) min J (x)

j
j


x∈R n (12)
j=1 k=0 p=1
s.t.G i (x) ⩽ 0,i = 1,2,··· M
式(6)的矩阵形式为
式中： J (x)为目标函数； G i (x)为约束函数.
Y = Hβ (7) QPSO算法具有较好的全局收敛性，但是容易出
式中： β为隐含层输出权值矩阵， 为网络输出样本矩 现早熟现象，陷入局部最优解. 因此，将SQP和QPSO
Y
阵， H为双隐含层输出矩阵. 结合，既能保证全局搜索能力，又能增强局部搜索能
DELM模型与传统ELM相比，具有随机参数少， 力. 当全局最优值变化量小于收敛阈值 τ时，则通过