Page 99 - 《摩擦学学报》2020年第5期

654 摩 擦 学 学 报 第 40 卷

8 4 No brake 8 4 No brake
Cross-coupled stiffness/(10 3 N/m) −4 0 l=4.25 Cross-coupled stiffness/(10 3 N/m) −4 0 n=90
l=2.25
n=30
l=3.25
n=60

−8 −8
0 50 100 150 200 250 300 0 50 100 150 200 250 300
Whirling frequency/Hz Whirling frequency/Hz
Fig. 18 Cross-coupled stiffness vs whirling frequency Fig. 21 Cross-coupled stiffness vs whirling frequency
for various swirl brake lengths for various swirl brake numbers
图 18 不同阻旋栅长度下交叉刚度k随涡动频率变化 图 21 不同阻旋栅数量下交叉刚度k随涡动频率变化

50
50
No brake
No brake
l=2.25 40 n=30
40
Effective damping/(N·s/m) 30 Effective damping/(N·s/m) 20
n=60
l=3.25
n=90
l=4.25
30
20
10
10
−10 0 −10 0
0 50 100 150 200 250 300 0 50 100 150 200 250 300
Whirling frequency/Hz
Whirling frequency/Hz
Fig. 19 Effective damping vs whirling frequency Fig. 22 Effective damping vs whirling frequency for
for various swirl brake lengths various swirl brake numbers
图 19 不同阻旋栅长度下有效阻尼C eff 随涡动频率变化 图 22 不同阻旋栅数量下有效阻尼C eff 随涡动频率变化

相比，不同阻旋栅数量下密封直接阻尼和有效阻尼均
27 No brake
n=30 增加，交叉刚度均降低；②随阻旋栅数量的增加，密封
Direct damping/(N·s/m) 21 ③阻旋栅周向个数从30增至60时，有效阻尼上升明
n=60
有效阻尼逐渐增大，特别是在低频时，增加较为明显；
24
n=90
显，而继续增加阻旋栅个数并不能显著提高有效阻
18
度变化幅度不大，过密的阻旋栅会减弱其对周向流动
15 尼，主要是由于随着阻旋栅周向个数的增加，交叉刚
的抑制作用.
0 50 100 150 200 250 300
Whirling frequency/Hz 3 结论
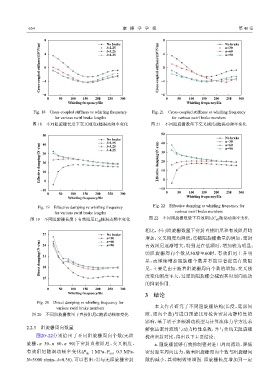
Fig. 20 Direct damping vs whirling frequency for
various swirl brake numbers 本文作者研究了不同阻旋栅结构(长度、底部间
图 20 不同阻旋栅数量下直接阻尼C随涡动频率变化 隙、周向个数)与进口预旋比对梳齿密封动静特性的
影响，基于转子多频涡动模型与计算流体力学方法求
2.2.3 阻旋栅周向数量 解梳齿密封流场与动力特性系数，并与传统无阻旋栅
图20~22分别给出了不同阻旋栅周向个数(无阻 梳齿密封对比，得出以下主要结论：

旋栅、n=30、n=60、n=90)下密封直接阻尼、交叉刚度、 a. 阻旋栅能够有效抑制密封进口周向流动、降低
有效阻尼随涡动频率变化(P =1 MPa、P =0.3 MPa、 密封腔室周向压力，随着阻旋栅周向个数与阻旋栅间
out
in
N=5000 r/min、 λ=0.36). 可以看出：①与无阻旋栅密封 隙的减小，其抑制效果增强. 阻旋栅长度增加到一定