Page 95 - 《摩擦学学报》2020年第5期

650 摩 擦 学 学 报 第 40 卷

Swirl brake
N ∑ N ∑
X direction :X = a cos(Ω i t),Y = b sin(Ω i t) (3)
i=1 i=1
Circumferential
N ∑ N ∑ Y
velocity location
Y direction :X = b cos(Ω i t),Y = a sin(Ω i t) (4) Z
i=1 i=1 Fig. 5 The location of the circumferential velocity
其中：X、Y分别表示X、Y方向的涡动位移，a、b分别为 distribution
图 5 周向速度取值位置
椭圆的长短半轴，Ω 为转子涡动速度.
i
表2给出了数值计算工况参数. 工质为空气(理想 12
气体)，采用标准k-ε湍流模型，涡动频率范围为20~ 10 No brake
s=0.25
280 Hz. 计算时给定进口总压1 MPa、总温293 K，出口 s=0.20
s=0.15
静压0.3 MPa，转子转速5 000 r/min. 稳态计算时，当动 8
−6
量、能量及湍流方程均方根残差降至10 以下，进出口 Circumferential velocity/(m/s) 6
流量差小于0.1%时可认为计算收敛. 非稳态计算时， 4
当转子X与Y方向受力呈周期性波动且不同周期内对 2
应点的受力波动小于0.1%，同时满足各方程均方根残
0
−6 30 31 32 33 34
差小于10 ，可认为计算收敛.
Position/mm
表 2 计算工况参数 Fig. 6 Circumferential velocity distribution for
Table 2 Calculation condition parameters various swirl brake clearances
图 6 不同阻旋栅间隙下密封腔周向速度分布
Parameter Specification
Working fluid air(ideal gas)
12
Wall adiabatic smooth wall
Turbulence model k-ε 10 No brake
l=2.25
Preswirl ratio, λ 0.36, 0.51, 0.81 l=3.25
Whirling speed, Ω i /Hz 20, 40, 60, …, 260, 280 8 l=4.25
Pressure inlet, P in /MPa 1
Pressure outlet, P out /MPa 0.3 Circumferential velocity/(m/s) 6
Inlet temperature, T/K 293 4
Rotational speed, ω/(r/min) 5 000
Time step, t/s 0.000 069 2
0
30 31 32 33 34
2 结果与分析 Position/mm

2.1 阻旋栅对密封流场影响 Fig. 7 Circumferential velocity distribution for
various swirl brake lengths
2.1.1 阻旋栅几何特性对周向速度分布的影响 图 7 不同阻旋栅长度下密封腔周向速度分布
为研究阻旋栅几何参数对密封内流体周向流动
的影响，分析第一个密封腔室中心的径向周向速度分 化情况. 当阻旋栅长度从2.25 mm增加到3.25 mm时，
布情况，如图5所示，比较阻旋栅间隙、长度及个数的 周向速度有显著降低，再继续增加阻旋栅长度(l=
变化对第一个腔室内周向速度影响. 4.25 mm)，则对周向速度影响较小.
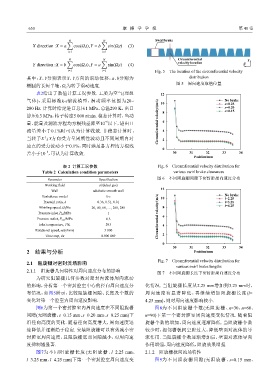
图6为第一个密封腔室内周向速度在不同阻旋栅 图8为不同阻旋栅个数(无阻旋栅、n=30、n=60、
间隙(无阻旋栅、s=0.15 mm、s=0.20 mm、s=0.25 mm)下 n=90)下第一个密封腔室周向速度变化情况. 随着阻
沿径向高度的变化. 随着径向高度增大，周向速度迅 旋栅个数的增加，周向速度逐渐降低. 当阻旋栅个数
速降低并逐渐趋于稳定. 安装阻旋栅可以有效减小密 较少时，相邻栅板间空腔过大，降低壁面对流体的导
封腔室周向速度，且阻旋栅底部间隙越小，对周向速 流作用. 当阻旋栅个数逐渐增加后，壁面对流体导向
度抑制越显著. 作用增强，周向速度降低，阻旋效果增强.
图7为不同阻旋栅长度(无阻旋栅、l=2.25 mm、 2.1.2 阻旋栅板间流场特性
l=3.25 mm、l=4.25 mm)下第一个密封腔室周向速度变 图9为不同阻旋栅间隙(无阻旋栅、s=0.15 mm、