Page 15 - 《摩擦学学报》2020年第3期

第 3 期 樊智敏, 等: 双渐开线齿轮传动的油膜刚度研究 281

1
1
半径、载荷与卷吸速度对油膜刚度、接触体刚度以及 — πm n — πm n
2 2
[6]
合成刚度的影响. Liu等 应用追踪法与能量转换机 E
α a
理，研究不同转速与润滑温度对齿轮润滑油膜刚度与
*
h a m n
[7]
阻尼的影响. Zhang等 提出线接触弹流润滑振动模
*
*
y d m n y a m n
*
型，研究载荷、卷吸速度与正弦波表面波幅对油膜刚 D l a m n
C
ρ g
[8]
*
度、接触刚度以及油膜阻尼的影响. Zhou等 建立齿轮 l d m n
*
h a m n
α d
传动油膜刚度与阻尼计算模型，研究接触力、转速与
齿数对油膜刚度的影响. 上述研究中，均未将油膜刚 B
度计算模型与齿轮实际啮合状况结合起来进行系统 ρ f A

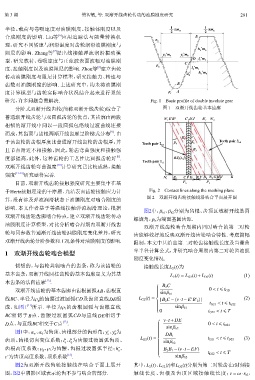
研究，许多问题急需解决. Fig. 1 Basic profile of double involute gear
分阶式双渐开线齿轮(简称双渐开线齿轮)综合了 图 1 双渐开线齿轮基本齿廓
普通渐开线齿轮与双圆弧齿轮的优点，其齿廓由两段 N 1 BE ′ 2 C D J B 1 ′ N 2 ′
′
′
′ ′
相错的渐开线中间以一段圆弧包络线过渡曲线连接
[9]
而成，其齿顶与齿根两渐开线齿廓呈阶梯式分布 . 由
B 4
于该齿轮的齿根厚度比普通渐开线齿轮的齿根厚，并 β b β b Teeth pair 3 rd
Teeth pair 2 nd
且节点附近不相接触，因此，轮齿弯曲强度和接触强 B 3
[9]
度都提高，此外，这种齿轮的工艺性比圆弧齿轮好 . RZ i (t, j)
Teeth pair 1 st
[10]
双渐开线齿轮弯曲强度 计算研究已比较成熟，接触
强度 [11-12] 研究亟待完善.
N 1 B 2 C P D E F B 1 N 2 GH J K
目前，双渐开线齿轮接触强度研究主要集中在基 P b P b

于Hertz接触理论的干摩擦、光洁表面齿轮接触应力计 Fig. 2 Contact lines along the meshing plane
图 2 双渐开线齿轮接触线沿啮合平面展开图
算，没有涉及弹流润滑状态下油膜刚度对啮合刚度的
影响. 本文作者基于等温线接触弹流润滑理论，根据
、
图2中， β b1 β b2分别为齿根、齿顶区域渐开线基圆
双渐开线齿轮齿廓啮合特点，建立双渐开线齿轮传动
螺旋角， p b 为端面基圆齿距.
油膜刚度计算模型，对比分析啮合周期内双渐开线齿
双渐开线齿轮啮合周期内同时啮合的第二对轮
轮与同参数普通渐开线齿轮油膜刚度变化差异，研究 齿能够较好地反映双渐开线齿轮啮合特性. 考虑篇幅
双渐开线齿轮分阶参数和工况条件对油膜刚度的影响. 限制，本文中只给出第二对轮齿接触线长度及当量曲
1 双渐开线齿轮啮合模型 率半径计算公式，并研究啮合周期内第二对轮齿油膜
刚度变化情况.
假想的，与齿轮共轭啮合的齿条，称为该齿轮的 接触线长度 L 2 (t)为
基本齿条，双渐开线圆柱齿轮的基本齿廓定义为其基 L 2 (t) = L G2 (t)+ L D2 (t) (1)
[13]
本齿条的法向齿廓 . 
 B 2 C
双渐开线齿轮的基本齿廓由齿根圆弧 AB、齿根直  0 < t ⩽ t G21



 sinβ b1



线 BC、半径为 的齿腰过渡圆弧 CD及齿顶直线 DE组 L G2 (t) =  [B 2 C −(v·t − E B 2 )] (2)
′
′
ρ g


 t G21 < t ⩽ t G22

[11]
成，如图1 所示. 半径为 ρ f 的齿根圆弧与齿根直线  sinβ b1


0 t G22 < t ⩽ T

BC相切于 点，齿腰过渡圆弧 CD与直线 DE相切于
B
 v·t + DE
[13]
D点、与直线 BC相交于 C点 .  0 < t ⩽ t D21




 sinβ b2

、
图1中， α α α d为齿顶、齿根部分的齿形角； 、 为 
y y
∗
∗


d
a

 DB 1

齿顶、齿根切向变位系数； l l 、 为齿腰过渡圆弧齿顶、 L D2 (t) =  t D21 < t ⩽ t D22 (3)
∗
∗

a
d
 sinβ b2



ρ g ρ f 为齿腰、齿根过渡圆弧半径； 、
齿根高度系数； 、 h ∗ 
 B 2 B 1 −(v·t − EF)

a 

 t D22 < t ⩽ T

[13]
c 为齿顶高度系数、顶系系数 . sinβ b2
∗
、
图2为双渐开线齿轮接触线在啮合平面上展开 其中： L 2 (t) L G2 (t)和 L D2 (t)分别为第二对轮齿在 t时刻接
图，图2中阴影区域表示轮齿不参与啮合的部分. 触线长度、齿根及齿顶区域接触线长度； v = ω·r b1 ，