Page 17 - 《摩擦学学报》2020年第3期

第 3 期 樊智敏, 等: 双渐开线齿轮传动的油膜刚度研究 283

润滑油等效黏度为 义接触线上的油膜刚度分布；将同一条名义接触线上

的油膜刚度进行叠加，得出该时刻的总油膜刚度.
τ/τ 0
η = η (11)
∗
sinh(τ/τ 0 ) 3.2 计算模型验证
式中： τ为润滑油剪切力； 为润滑油特征剪切力. 为了验证双渐开线齿轮传动油膜刚度计算模型
τ 0
载荷平衡方程为 的正确性，本文中将分别对弹流润滑求解结果以及油
∫ 膜刚度计算结果进行验证. 表1所示为根据文献[16]所
x out
w = pdx (12)
述参数，分别采用D-H经验公式、文献[16]所述模型和
x in
；
式中： w为单位线载荷，定义为 w = F/L F为某瞬时啮 本文模型求解的中心油膜厚度、最小油膜厚度数值大
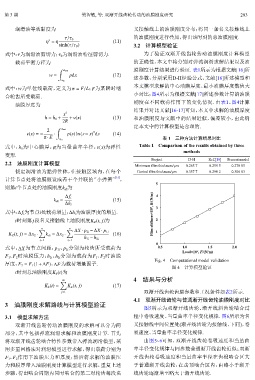
小对比；图4所示为根据文献[17]所述参数计算的油膜
合轮齿所受载荷.
刚度在不同载荷作用下的变化情况. 由表1、图4计算
油膜厚度为
结果并对比文献[16-17]可知，本文中求解的油膜厚度
x 2
h = h 0 + +v(x) (13) 和油膜刚度与文献中的结果近似，偏差较小，由此确
2R
定本文中的计算模型是合理的.
∫
2 x out
2
v(x) = − · p(s)ln(s− x) ds (14)
π· E 表 1 三种方法计算结果对比
x in
式中： h 0为中心膜厚， 为当量曲率半径， v(x)为弹性 Table 1 Comparison of the results obtained by three
R
methods
变形.
Project D-H Ref.[16] Present model
2.2 油膜刚度计算模型
Minimum film thickness/μm 0.265 7 0.259 5 0.270 85
假定润滑油为黏弹性体，在接触区域内，在每个 Central film thickness/μm 0.357 7 0.290 2 0.306 83
[15]
计算节点处将油膜假设成若干个并联的“小弹簧” ，
5
则第i个节点处的油膜刚度k 为
di
∆f i 4
k di = (15)
∆h i 3
式中： ∆f i 为节点 i处载荷增量； ∆h i为油膜厚度的增量. Film stiffness×10 6 , K/(N/m)
t时刻第 j段名义接触线上油膜刚度 K Z (t, j)为 2
n ∑ n ∑
∆X · p 2i −∆X · p 1i 1
K Z (t, j) = ∆x 2 · k di = ∆x 2 · (16)
h 1i −h 2i
i=1 i=1
0
、
式中： ∆X 为节点间距； p 1i p 2i 分别为轮齿所受载荷为 0.5 1.0 1.5 2.0
Load×10 , F/(N/m)
6
F 1 F 2 时油膜
、
F 1 F 2 时油膜压力； h 1i h 2i 分别为载荷为 、
、
Fig. 4 Computational model validation
厚度， F 2 = F 1 (1+∆F) ∆F 为载荷增量因子.
，
图 4 计算模型验证
t时刻总油膜刚度 K b (t)为
4 结果与分析
m ∑
K b (t) = K Z (t, j) (17)
j=1 双渐开线齿轮齿廓参数和工况条件如表2所示.
4.1 双渐开线齿轮与普通渐开线齿轮油膜刚度对比
3 油膜刚度求解路线与计算模型验证
图5所示为双渐开线齿轮、渐开线斜齿轮啮合过
3.1 模型求解方法 程中卷吸速度、当量曲率半径变化规律. 图6所示为名
双渐开线齿轮传动油膜刚度的求解可以分为两 义接触线中间位置处(渐开线齿轮为接触线，下同)，卷
部分，其中包括弹流润滑求解和油膜刚度计算. 首先 吸速度、当量曲率半径变化规律.
将双渐开线齿轮啮合特性参数带入弹流润滑模型，采 由图5~6可知，双渐开线齿轮卷吸速度和当量曲
用多重网格法对润滑模型进行求解，得出载荷分别为 率半径变化规律与同参数普通渐开线齿轮近似；双渐
、
F 1 F 2 作用下油膜压力和厚度；然后将求解的油膜压 开线齿轮卷吸速度和当量曲率半径在齿根啮合区大
力和膜厚带入油膜刚度计算模型进行求解，重复上述 于普通渐开线齿轮，在齿顶啮合区内，由略小于渐开
步骤，得出啮合周期内同时啮合的第二对轮齿每段名 线齿轮逐渐增至略大于渐开线齿轮.