Page 119 - 《高原气象》2021年第5期
P. 119
高 原 气 象 40 卷
1080
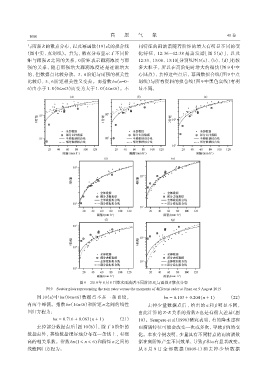
与雨强 R 的散点分布,以及幂函数(19)式的拟合线 同特征的雨滴谱随着阶矩的增大有明显不同的变
(图中实、点划线)。首先,散点分布显示了不同阶 化特征,12:36-12:38 是蒸发谱[图 5(a)],以及
矩与雨强 R 之间的关系,0 阶矩表示雨滴浓度与雨 12:53、13:08、13:10[分别见图 5(c)、(b)、(d)]有较
强的关系,随着雨强增大雨滴浓度还是逐渐增大 多大粒子,所以在高阶矩时增大的很快(图 9 中空
的,但数据点比较分散。3、4 阶矩与雨强的相关性 心圆点),去掉这些点后,幂函数拟合线(图 9 中点
比较好,5、6 阶矩相关性又变差。而指数 bn(n=0~ 划线)与所有资料的拟合线(图 9 中黑色实线)有明
6)由小于 1. 0(0≤n≤3)而变为大于 1. 0(4≤n≤6)。不 显不同。
图9 2019年8月9日降水雨滴谱不同阶矩Ω 与雨强R散点分布
n
图9 Scatter plots representing the rain rates versus the moments of different order at Jinan on 9 Augest 2019
图 10(a)中 bn(0≤n≤6)数据点不在一条直线, bn = 0.103 + 0.204(n + 1) (22)
有两个峰值。指数 bn(1≤n≤6)和阶矩 n 之间的线性 去掉少量数据点后,给出的 α 和 β 明显不同,
回归方程为: 由此计算的 Z-R 关系的指数 b 也是有很大差异(图
bn = 0.716 + 0.063(n + 1) (21) 10)。Sempere et al(1998)研究表明,有的降水过程
去掉部分数据点后[图 10(b)],除了 0 阶矩的 雨滴谱特征可能会改变一次或多次,导致 β 值的变
数据点外,其他数据很好地分布在一条线上,有很 化。本次个例表明,少量具有不同特点的雨滴谱数
高的相关系数。指数 bn (1 ≤ n ≤ 6) 和阶矩 n 之间的 据在高阶矩产生不同效果,导致 β和 α有显著改变。
线性回归方程为: 从 8 月 9 日 全 部 数 据(0809-1)和 去 掉 少 量 数 据