Page 94 - 《爆炸与冲击》2026年第01期

第 46 卷 杜青松，等： 深海水下爆炸冲击波载荷及气泡脉动特性研究 第 1 期
Å 2 ã
∂φ R v 1
= − H + + R ˙ 2 Ä ä (17)
∂t (r, t) |r| 4 2 |r|−R
R, t−
c
式中：各变量的意义同气泡脉动方程，这里的 H=(p−p )/ρ。将式 (17) 代入到式 (15) 中可得：
a
´
ß Å 2 ã 2 ï Å 2 ãò 2
R v 1 1 R |r|−R v 1
˙
p = p a +ρ H + + R ˙ 2 − RR+ H + + R ˙ 2 (18)
|r| 4 2 2 |r| 4 c 4 2 Ä |r|−R ä
R, t−
c
由式 (18) 即可计算在任意位置的压力场，值得注意的是，t 时刻距气泡中心距离为 r 的流场中的压
力扰动是由较早时刻的气泡引起的，因为在 t−(|r|−R)/c 时刻，气泡半径 R 以内区域是不参与压力场计算的。
1.3 模型参数
TNT 炸药的状态方程采用 JWL 状态方程：
Å 3 ã Å 3 ã Å ã −3(ω+1)
R R R
p g = Aexp −R 1 + Bexp −R 2 +c (19)
R 3 c R 3 c R c
式中：R 为气泡半径，R 为炸药装药半径，A、B、
c
表 1 TNT 炸药的材料参数
2 ω 为材料参数。具体参数如表 1 所示。
1 Table 1 Material parameters of TNT
R 、R 和
炸药的密度为 1 630 kg/m 。
3
A/GPa B/GPa R 1 R 2 ω
水的状态方程选用 Tammann 状态方程，其
371.2 3.231 4.15 0.95 0.3
常见形式为：
p = ρe(γ −1)− p w γ (20)
3
式中：水的密度 ρ=1 024 kg/m ，e 为质量内能，绝热指数 γ=7.15，参考压力 p =330.9 MPa。
w
2 模型精度与有效性验证
为验证所采用的 Zhang 方程理论模型的计算准确性，同时对比分析其与传统模型的优势，本文中选
取 Gao 等 [15] 基于压力罐试验所得的部分试验数据作为参考，依据其设定的水深 500 m，爆距 0.49 m，装药

量 10 g 工况条件，代入 Zhang 方程进行计算，并
25 Test [15]
结合 Geers-Hunter 模型的计算结果进行对比，所 Zhang equation
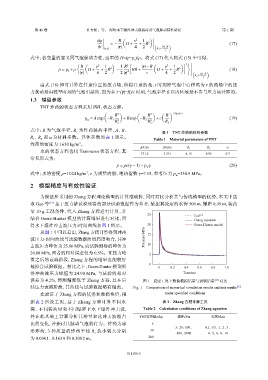
得水下爆炸冲击波压力-时间曲线如图 1 所示。 20 Geers-Hunter model
从图 1 中可以看出，Zhang 方程计算得到冲击 15
波压力-时间曲线与试验数据曲线高度吻合，其冲 Pressure/MPa
击波压力峰值为 25.86 MPa，而试验测得的峰值为 10
26.00 MPa，两者的相对误差仅为 0.5%。在压力峰 5
值之后的衰减阶段，Zhang 方程的结果也能较好
0
地拟合试验数据。相比之下，Geers-Hunter 模型所 0 0.2 0.4 0.6 0.8 1.0
得冲击波压力峰值为 24.90 MPa，与试验的相对 Time/ms
误差为 4.2%，预测精度低于 Zhang 方程，且在后 图 1 设定工况下数值模拟结果与试验结果 [15] 对比
续压力衰减阶段，其曲线与试验数据略有偏离。 Fig. 1 Comparison of numerical simulation results and test results [15]
在验证了 Zhang 方程的优势和准确性后，根 under specified conditions

据表 2 所设工况，基于 Zhang 方程计算不同水 表 2 Zhang 方程计算工况
深、不同装药量和不同爆距下水下爆炸冲击波， Table 2 Calculation conditions of Zhang equation
并在此基础上计算分析其冲量和比冲击波能占 TNT装药量w/kg 爆距D/m 水深h/km
比的变化，并探讨其脉动气泡的行为。炸药为球 5
5、20、100、 0.1、0.5、1、2、3、
形炸药，3 种质量的炸药半径 R 从小到大分别 30
c
400、2 000 4、5、6、8、10
为 0.090 1、0.163 8 和 0.308 2 m。 200

011106-5