Page 48 - 《爆炸与冲击》2025年第12期

第 45 卷 郑 成，等： 基于板厚补偿的不同型号钢制靶板在舱内爆炸载荷作用下的等效方法 第 12 期

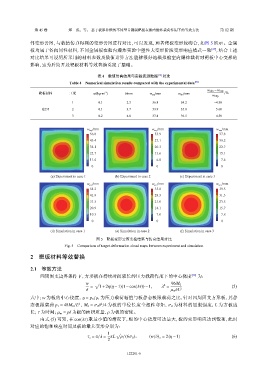
件变形云图，与数值仿真得到的变形云图进行对比，可以发现，两者靶板变形较吻合，如图 5 所示。金属
板均属于各向同性材料，不同金属板在舱内爆炸实验中塑性大变形阶段变形响应模式一致 [27] ，结合上述
对比结果可说明所采用的材料参数及数值计算方法能够很好地模拟舱室内爆炸载荷对靶板中心变形的
影响，这为后续开展靶板材料等效替换奠定了基础。

表 4 数值仿真结果与实验实测数据 [12] 对比
Table 4 Numerical simulation results compared with the experimental data [12]
w sim −w exp
−3
靶板材料 工况 α/(kg·m ) δ/mm w exp /mm w sim /mm /%
w exp
1 0.1 2.3 56.8 54.2 −4.58
Q235 2 0.1 3.7 33.9 35.8 5.60
3 0.2 4.8 37.8 39.5 4.50

w exp /mm w exp /mm w exp /mm

56.8 33.9 37.8
45.4 27.1 30.2
34.1 20.3 22.7
22.7 13.6 15.1
11.4 6.8 7.6
0 0 0

(a) Experiment in case 1 (b) Experiment in case 2 (c) Experiment in case 3
w sim /mm w sim /mm w sim /mm
54.2 35.8 39.5
41.9 28.3 31.3
31.5 21.0 23.5
20.9 14.1 15.7
10.5 7.0 7.8
0 0 0

(d) Simulation in case 1 (e) Simulation in case 2 (f) Simulation in case 3

图 5 靶板变形云图实验结果与仿真结果对比
Fig. 5 Comparison of target deformation cloud maps between experiment and simulation
2 靶板材料等效替换

2.1 等效方法
四周固支边界条件下，方形板在持续时间较长的压力载荷作用下的中心挠度 [28] 为：
w √ 2 96M 0
= 1+2η(η−1)(1−cos(λτ))−1, λ = (5)
δ µ m δL 2
式中：w 为板的中心挠度， η = p 0 /p 1 为压力载荷幅值与板静态极限载荷之比，针对四周固支方形板，其静
p 1 = 48M 0 /L 2 2 σ 0 为材料的屈服强度，L 为方板边
态极限载荷 ， M 0 = σ 0 δ /4 为板的单位长度全塑性弯矩，
ρ 为板的密度。
长； τ 为时间； µ m = ρδ 为板的面积质量，
由式 (5) 可知，在 cos(λτ) 取最小值的情况下，板的中心挠度可达最大，板的变形响应达到饱和，此时
对应的饱和响应时间及板的最大变形分别为：
1 √
τ s = π/λ = πL ρ/(6σ 0 )， (w/δ) s = 2(η−1) (6)
2

122201-6