Page 46 - 《爆炸与冲击》2025年第12期

第 45 卷 郑 成，等： 基于板厚补偿的不同型号钢制靶板在舱内爆炸载荷作用下的等效方法 第 12 期

1.1.1 材料力学性能参数
靶板材料为 Q235 钢、Q355 钢、907A 钢和 921A 钢，靶板材料属性具体参数如表 1 所示，表中 ρ 为
0
密度，E 为弹性模量，μ 为泊松比，A 为静态屈服应力，B 为硬化系数， n 为硬化指数， C 为应变率参数，m 为
热软化指数。在爆炸载荷作用下，结构材料将历经大变形、高应变率和高温过程，其材料的动态屈服应
力采用 Johnson-Cook 模型来描述，即：
ï Å ã m ò
( )[ ( )] T −T r
σ eq = A+ Bε n eq 1+C ln ˙ ε eq /˙ ε 0 1− (1)
T m −T r
ε ˙ ε 0 为参考应变率，T 为绝对温
eq
式中： σ eq 为材料的等效应力， 为等效塑性应变， ˙ ε eq 为当前塑性应变率，
度，T 为室温，T 为熔化温度。
r
m

表 1 靶板结构材料的本构参数
Table 1 Constitutive parameters for target plate structural materials
−3
靶板材料 ρ 0 /(kg·m ） E/MPa μ A/MPa B/MPa n C m
Q235 [20-21] 7 850 206 0.28 293.8 230.2 0.578 0.065 2 0.706
Q355 [22-23] 7 850 206 0.28 339.45 405 0.403 0.02 0.659
907A [24-25] 7 850 220 0.3 580 395 0.62 0.055 1.03
921A [25-26] 7 870 212 0.31 651 395 0.62 0.055 1.03

对舱室内的空气采用理想气体状态方程：

p = (γ −1)ρe (2)
3
γ 、ρ 和 γ =1.4，ρ=1.225 kg/m ，e=206.8 J/g。
式中： e 分别为空气的比热比、密度和比内能，取值分别为
1.1.2 有限元模型的边界条件与接触设置
对空气域均采用 Euler 单元进行离散，具体尺寸为 1 000 mm×400 mm×400 mm，靠近靶板的一侧向外
延伸 100 mm。选取爆源处测点的压力时程进行 Euler 网格收敛性分析，考虑到计算规模和精度要求，最
终选取的 Euler 单元尺寸为 10 mm×10 mm×10 mm。再选取经验证的 Euler 单元尺寸进行受载区域
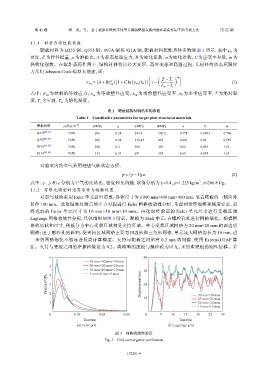
Lagrange 网格收敛性分析，具体结果如图 3 所示。靶板为 Shell 单元，在螺栓孔处进行网格细化。根据网
格的形状和尺寸，靶板分为中心受载区域和受夹持区域。中心受载区域网格为 20 mm×20 mm 的四边形
网格；由于螺栓孔的影响，受夹持区域网格主要为四边形和三角形网格，单元最大网格边长为 10 mm，进
一步的网格细化不能显著提高计算精度。夹持与靶板之间留有 0.2 mm 的间隙，使用 External GAP 算
法。夹持与靶板之间的摩擦因数设为 0.2。将模型的压板与螺栓设为固支，来约束靶板的刚性位移。采

6 40

30 mm×30 mm×30 mm
5 20 mm×20 mm×20 mm
10 mm×10 mm×10 mm 30
5 mm×5 mm×5 mm
4
Pressure/GPa 3 2 Displacement/mm 20

25 mm×25 mm
1 10 30 mm×30 mm
20 mm×20 mm
15 mm×15 mm
0 0.02 0.04 0.06 0 5 10 15 20 25 30
Time/ms Time/ms
(a) Euler grid (b) Lagrange grid

图 3 网格收敛性验证
Fig. 3 Grid convergence verification

122201-4