Page 71 - 《爆炸与冲击》2025年第6期

第 45 卷 张 旭，等： 高温大理岩的动态能量耗散机理及破坏特征 第 6 期

2
p max = −ρcv 0 /2 c = E/ρ (2)
式中：c 为波速，ρ 为杆件密度，E 为杆件弹性模量，v 为冲击速度。
0
根据上述试验数据，分别设置冲击速度为 10.0、11.5、12.5、13.5、14.5 m/s，分别对应施加入射波应力
幅值为 200、225、250、275、300 MPa，延时 200 μs 的半正弦波。

1.3 可靠性验证
为了定量分析高温大理岩动态压缩试验的动态平衡状况，通过动态应力平衡因子 η 随时间演化趋
势反映入射杆与透射杆两端应力的差异：
2[σ i (t)+σ r (t)−σ t (t)]
η = (3)
σ i (t)+σ r (t)+σ t (t)
σ i (t) σ r (t) σ t (t) 分别为入射应力、反射应力、透射应力。
式中： 、 、
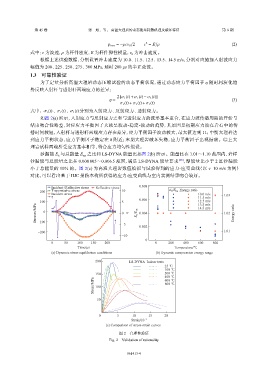
如图 2(a) 所示，入射应力与反射应力之和与透射应力的波形基本重合，在应力波传播周期的开始与
结束吻合性略差，对应应力平衡因子大致呈波动-稳定-波动的趋势，其原因是初期应力波在岩石中的传
播时间较短，入射杆与透射杆两端应力存在差异，应力平衡因子波动较大，最大值达到 11；中期大理岩达
到应力平衡状态，应力平衡因子稳定在 0 附近；末期大理岩破坏失稳，应力平衡因子出现振荡。综上大
理岩试样两端所受应力基本相等，符合应力均匀性假设。
沙漏能 E 与总能量 E 之比和 LS-DYNA 能量比如图 2(b) 所示。能量比在 1.01～1.10 范围内，岩样
t
h
to
沙漏能与总能量之比在 0.000 805～0.006 5 范围，满足 LS-DYNA 能量要求 [28] ，即能量比小于 2 且沙漏能
小于总能量的 10% 的。图 2(c) 为高温大理岩数值模拟与试验得到的应力-应变曲线（以 v=10 m/s 为例）
对比，可以看出基于 HJC 损伤本构所获得的应力-应变曲线与室内实测结果吻合较好。

0.008
Incident+Reflective stress Reflective stress
200 Transmissive stress 10 E h /E tot Energy ratio
Incident stress 10.0 m/s 1.03
η 11.5 m/s
100 5 0.006 12.5 m/s
13.5 m/s
Stresses/MPa 0 0 η E h /E tot 0.004 14.5 m/s 1.02 Energy ratio

−100
−5
0.002
−200 1.01
−10
0
0 50 100 150 200 0 200 400 600 800
Time/µs Temperature/℃
(a) Dynamic stress equilibrium conditions (b) Dynamic compression energy range

200 LS-DYNA Indoor tests
25 ℃
100 ℃
150 200 ℃
400 ℃
Stress/MPa 100 800 ℃
600 ℃

50

0 5 10 15 20
Strain/10 −3
(c) Comparison of stress-strain curves

图 2 合理性验证
Fig. 2 Validation of rationality

061413-4