Page 70 - 《爆炸与冲击》2025年第6期

第 45 卷 张 旭，等： 高温大理岩的动态能量耗散机理及破坏特征 第 6 期

参数确定方法成熟，参数数量相对较少，大多参数可基于静态试验的基本物理参数根据经验公式获得，
具备准确性的同时平衡了冗杂的工作量。
大理岩的 HJC 本构模型涉及 21 个参数，为保证数值模拟的科学有效性，本文依据张志华 [23] 的高温
静态物理实验获取的反映高温损伤的物理力学参数，结合相关岩石的 HJC 本构模型参数确定方法 [24-25]
进行初步拟定，然后经过大量试错优化，最终调整确定相关参数，见表 1 和表 2。为凸显温度对模型参数
的影响，分别设置温度无影响参数和温度影响参数两类。

表 1 高温大理岩温度无影响参数
Table 1 Temperature unaffected parameters of high temperature marble
A B N C p lock /GPa ˙ ε 0/s −1 S max
0.355 2.003 0.849 0.008 1.2 0.001 6.0
K 1 /GPa K 2 /GPa K 3 /GPa D 1 D 2 破坏类型 ε f,min
44 39 3.8 0.04 1 2.0 0.03
k
注：A 为归一化黏性强度系数, B 为归一化压力硬化系数, N 为压力硬化指数, C 为应变率系数, p loc 为压实点静水压力, ˙ ε 0 为参考应变
率, S ma 为归一化最大强度, K 1 、K 2 、K 3 为压力参数, D 1 、D 2 损伤参数, ε f,mi 为材料断裂时最小塑性应变。
n
x

表 2 高温大理岩受温度影响参数
Table 2 Parameters of high temperature marble affected by temperature
−3
温度/℃ 密度/(g·cm ) 抗压强度/MPa 剪切模量/GPa 抗拉强度/MPa 压溃点静水压力/MPa 压溃点体积应变/10 −2 压实点体积应变/10 −2
25 2.73 73.6 14.2 6.82 24.5 0.19 2.22
100 2.74 83.7 13.3 6.64 27.9 0.15 2.19
200 2.72 51.5 12.1 6.44 17.2 0.12 2.03
400 2.58 42.9 9.40 6.80 14.3 0.12 2.03
600 2.67 54.4 7.93 6.48 18.1 0.19 2.04
800 1.86 34.2 1.89 3.40 11.4 0.49 2.04

1.2 数值模型建立

为探究高温下大理岩动态破坏过程，本文 表 3 杆件有限元模型参数
利用 ANSYS/LS-DYNA 数值模拟模块建立大理 Table 3 Parameters of finite element
岩与 SHPB 杆件的有限元模型。入射杆和透射 model for rods
杆选用线弹性模型，相关尺寸参数与材料参数见 入射杆 透射杆 直径/ 密度/ 弹性模量/
泊松比
表 3。大理岩尺寸为 ∅ 50 mm×40 mm 的圆柱形 长度/m 长度/m mm (g·cm ) GPa
−3
标准试样，选用 HJC 损伤本构模型。杆与大理 1.0 1.0 75 7.80 211 0.3
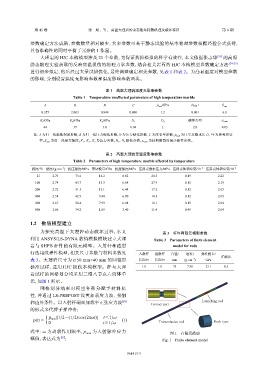
岩试样的网格划分均采用三维八节点六面体单
元，如图 1 所示。
网 格 划 分 结 束 对 模 型 各 部 分 赋 予 材 料 属
性，并通过 LS-PREPOST 设置加载应力波、接触
和边界条件。以入射杆端面加载半正弦应力波 [26] Contact part Launching rod
的形式来代替子弹冲击：
ß
p max [1/2−(1/2)cos(2πωt)] t＜1/ω
p(t) = (1) Transmissive rod Rock type
0 t≥1/ω
式中：ω 为动载作用频率，p ma x 为入射脉冲应力 图 1 有限元模型
幅值，表达式为 [27] ： Fig. 1 Finite element model

061413-3