Page 75 - 《爆炸与冲击》2025年第6期
P. 75
第 45 卷 张 旭,等: 高温大理岩的动态能量耗散机理及破坏特征 第 6 期
−5
2
ε peak = 7.891 48−0.008 94T +2.379 03×10 T 2 R = 0.959 (7)
−3
T 的单位为 ε peak 的单位为 10 。
式中: ℃,
与峰值应力不同,由于大理岩组分及微观
10.0 m/s 11.5 m/s 12.5 m/s
裂隙分布的随机性,温度低于 400 ℃ 时,同一冲
20 13.5 m/s 14.5 m/s
击速度下的峰值应变随温度的增大存在一定的 Average peak strain
Fit curve
离散性;温度超过 400 ℃ 后,同一冲击速度下的 15
峰值应变随温度的增加而增大。温度低于 100 ℃ Stain/10 −3 10
时,相同冲击速度下的峰值应变随温度变化相对
较 小 ; 当 温 度 达 到 200 ℃ 时 , 峰 值 应 变 显 著 增 5
强,与 100 ℃ 时相比,v=10.0, 11.5, 12.5, 13.5,
0
14.5 m/s 时的峰值应变分别增加了 81%、39%、 0 200 400 600 800
40%、15% 和 13%;而当温度达到 400 ℃ 时,峰值 Temperature/℃
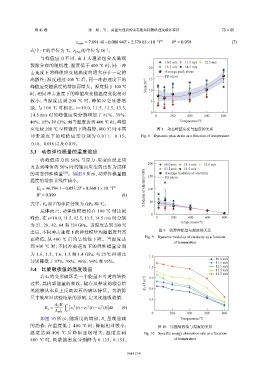
应变较 200 ℃ 呈轻微的下降趋势;800 ℃ 时不同 图 8 动态峰值应变与温度的关系
冲 击 速 度 下 的 峰 值 应 变 分 别 为 0.011、 0.15、 Fig. 8 Dynamic peak strain as a function of temperature
0.18、 0.018 以及 0.019。
3.3 动态弹性模量的温度效应
将峰值应力的 50% 与应力-应变曲线上应
200 10.0 m/s 11.5 m/s 12.5 m/s
力达到峰值的 50% 时的轴向应变的比作为试样 13.5 m/s 14.5 m/s
的动态弹性模量 [29] 。如图 9 所示,动弹性模量随 150 Average modulus of elasticity
Fit curve
温度的增加非线性减小:
−7
E d = 46.794 3−0.053 2T +9.360 1×10 T 2 Modulus of elasticity/GPa 100
2
R = 0.999 (8)
T 的单位分别为 GPa 和 ℃。 50
式中: E d 和
总体而言,动弹性模量约在 100 ℃ 时达到
0
峰值,在 v=10.0, 11.5, 12.5, 13.5, 14.5 m/s 时分别 0 200 400 600 800
Temperature/℃
为 27、28、42、64 和 124 GPa。当温度达到 200 ℃
之后,不同冲击速度下的弹性模量均随温度升高 图 9 动弹性模量与温度的关系
而降低,从 400 ℃ 后均呈线性下降。当温度达 Fig. 9 Dynamic modulus of elasticity as a function
of temperature
到 800 ℃ 时,不同冲击速度下的弹性模量分别
为 1.6、1.5、1.6、1.5 和 1.4 GPa,与 25℃ 时相比 1.5
分别降低了 97%、98%、96%、94% 和 95%。 10.0 m/s
11.5 m/s
1.2 12.5 m/s
3.4 比能吸收值的温度效应 13.5 m/s
14.5 m/s
岩石的变形破坏是一个能量不可逆的转换 0.9
过程,其内部能量的吸收、储存及释放的综合结 E V /(J·m −3 )
果能够从本质上反映岩石的破坏特征。为消除 0.6
尺寸效应对试验结果的影响,定义比能吸收值: 0.3
A G E w t [ 2 2 2 ]
E v = ε i (t)−ε r (t)−ε t (t) dt (9)
0 200 400 600 800
A 0 l 0 0
如图 10 所示,随温度的增加,E 呈现递减 Temperature/℃
v
的趋势,在温度低于 400 ℃ 时,降幅相对较小; 图 10 比能吸收值与温度的关系
温 度 达 到 400 ℃ 后 降 幅 逐 级 增 大 ; 温 度 达 到 Fig. 10 Specific energy absorption rate as a function
800 ℃ 时,耗散能密度分别降为 0.125、0.151、 of temperature
061413-8