Page 53 - 《爆炸与冲击》2023年第2期

第 43 卷 李国强，等： 冲击荷载作用下滤波混凝土的动态响应与层裂损伤数值研究 第 2 期

[18] 为：
混凝土的压缩动态强度增强系数 φ c
ß 1.026α
) −1
(˙ε/˙ε s ˙ ε≤30s 表 3 滤波混凝土模型的几何参数
φ c = 1/3 −1 (12)
γ s (˙ε/˙ε s ) ˙ ε＞30s
Table 3 Geometric parameters of the filter concrete model
[19] 为：
混凝土的拉伸动态强度增强系数 φ t L/mm D/mm l/mm r/mm T/mm
500 74 75 22 2
ß δ
) −1
(˙ε/˙ε s ˙ ε≤1s
φ t = 1/3 −1 (13)
β(˙ε/˙ε s ) ˙ ε＞1s
s lgβ = 6δ−2 δ = 1/(1+8 f cs / f c0 ) ；
c0
式中： lg γ s = 6.156α−2 α = 1/(5+9f cs / f c0 ) ，f =10 MPa，f 为静态抗压强度； ，
，
c
−6 −1
˙ ε s = 10 s 为静态应变率。
2.1.3 单元侵蚀准则
在模拟中，金属球、弹性层和混凝土基体的单元类型均为单点积分的六面体拉格朗日实体单元，各
单元之间为共节点连接以传递力和位移。为了模拟混凝土材料在荷载作用下的剪切、破碎和层裂等破
坏效果，通常采用侵蚀算法（Add_Erosion） [12, 20] 。在对不同侵蚀准则进行了大量模拟研究后，最终以
0.01 的最大主应变作为混凝土材料的侵蚀准则。
2.2 模型有效性验证
本文中，滤波混凝土模型尺寸设计基于 Wu 等 [21] 的混凝土试件。为验证数值模型的有效性，将该滤
波混凝土模型替换为 Wu 等 [21] 实验研究中的同尺寸普通混凝土模型。对该模型施加如图 7 所示的实验
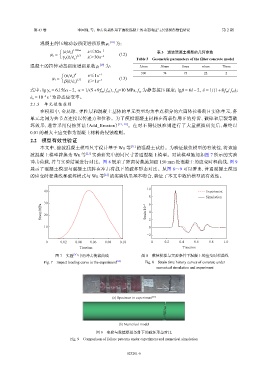
冲击荷载，并与实验结果进行对比。图 8 展示了距离荷载施加面 150 mm 处混凝土的应变时程曲线，图 9
展示了混凝土模型与混凝土试件在冲击荷载下的破坏形态对比。从图 8～9 可以看出，普通混凝土模型
的应变时程曲线和破坏模式与 Wu 等 [21] 的实验结果基本吻合，验证了本文中数值模型的有效性。

10
40 Experiment
8 Simulation
30 6
Stress/MPa 20 Strain/10 −4 4 2

10 0
−2

0 0.02 0.04 0.06 0.08 0.10 0 0.2 0.4 0.6 0.8 1.0
Time/ms Time/ms

图 7 实验 [21] 中的冲击荷载曲线 图 8 数值模拟与实验条件下混凝土的应变时程曲线
Fig. 7 Impact loading curve in the experiment [21] Fig. 8 Strain time history curves of concrete under
numerical simulation and experiment

(a) Specimen in experiment [21]

(b) Numerical model

图 9 实验与数值模拟条件下的破坏形态对比
Fig. 9 Comparison of failure patterns under experiment and numerical simulation

023201-6