Page 58 - 《爆炸与冲击》2023年第2期

第 43 卷 李国强，等： 冲击荷载作用下滤波混凝土的动态响应与层裂损伤数值研究 第 2 期

抗冲击能力。图 21 展示了弹性层的弹性模量不 100
同时，滤波混凝土模型截面 S0 处单元 E1 和 E2
的位移响应曲线。通过对比可以看出，过软的弹 80
性层会增大金属球与混凝土基体的相对位移，导
致金属球的振动速度和频率大幅降低，这在一定 Energy proportion/% 60
程度上降低了弹性层对应力的传递速度以及滤
波单元的储能效率。而过硬的弹性层则会限制 40
E=4.7 MPa E=470 MPa
金属球与基体之间的相对运动，在一定程度上影 E=47 MPa E=4 700 MPa
响滤波单元与基体之间的能量转化，从而降低滤 0 0.5 1.0 1.5
波单元的储能效果。 Time/ms

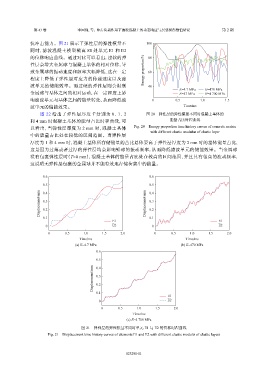
图 22 给出了弹性层厚度 T 分别为 0、1、2 图 20 弹性层的弹性模量不同时混凝土基体的
和 4 mm 时混凝土基体的能量占比时程曲线，可 能量占比时程曲线
以看出，当弹性层厚度为 2 mm 时，混凝土基体 Fig. 20 Energy proportion time history curves of concrete matrix
with different elastic modulus of elastic layer
中的能量占比处在较低的区间范围。当弹性层
厚度为 1 和 4 mm 时，混凝土基体所存储能量的占比总体要高于弹性层厚度为 2 mm 时的基体能量占比，
这是因为过薄或者过厚的弹性层均会影响铅球的振动频率，从而降低滤波单元的储能效果。当金属球
没有包裹弹性层时（T=0 mm），混凝土基体的能量占比处在较高的区间范围，并且具有很高的波动频率，
这说明无弹性层包裹的金属球并不能有效地存储荷载中的能量。

0.6 0.6

0.5 0.5

0.4
Displacement/mm 0.3 Displacement/mm 0.3
0.4
0.2
0.2
0.1 0.1
E1 E1
0 E2 0 E2
0 0.5 1.0 1.5 2.0 0 0.5 1.0 1.5 2.0
Time/ms Time/ms
(a) E=4.7 MPa (b) E=470 MPa
0.6
0.5

Displacement/mm 0.3
0.4

0.2
0.1
E1
0 E2
0 0.5 1.0 1.5 2.0
Time/ms
(c) E=4 700 MPa
图 21 弹性层的弹性模量不同时单元 E1 与 E2 的位移时程曲线
Fig. 21 Displacement time history curves of elements E1 and E2 with different elastic modulis of elastic layers

023201-11