Page 297 - 《软件学报》2020年第10期

金耀 等:距离约束的网格曲面曲线设计方法 3273

104ms,而最近点策略迭代 101 次,耗时 431ms.因此,前者能在不影响结果的前提下有效地提升效率.本文同时比较了
不同邻域大小对结果的影响,如图 5(b)所示(其中的红点为插值点,下同).由图可见:1-环邻域结果与其他结果有一定
差异,而 2-环与 3-环邻域的结果几无区别,三者的迭代次数分别为 126、95 与 88 次.由此说明,r 对算法收敛快慢有
一定影响.这是由于 r 较小时,曲线移动的步长相应减少,因此需要更多的迭代次数到达极小值点;而当 r≥2 时,其结
果差异较小,虽然能在一定程度上加快收敛,但同时也意味着将增加局部搜索次数.综合权衡算法效率,本文将 r 默
认设置为 2.

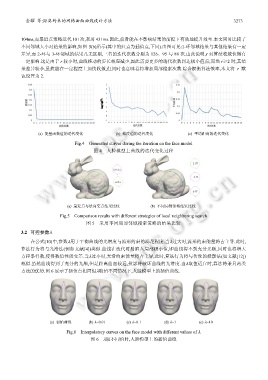
(a) 能量函数值的迭代变化 (b) 梯度值的迭代变化 (c) 平均距离的迭代变化
Fig.4 Generated curves during the iteration on the face model
图 4 人脸模型上曲线的迭代变化过程

(a) 最近点与法向交点结果比较 (b) 不同局部邻域结果比较

Fig.5 Comparison results with different strategies of local neighboring search
图 5 采用不同局部邻域搜索策略的结果比较
3.2 可控参数λ
在公式(10)中,参数λ用于平衡曲线的光滑度与流形约束的满足程度.当λ过大时,流形约束能量将占主导.此时,
算法行为将与光滑法(例如文献[4])类似.曲线在迭代时易陷入局部极小值,即曲线得不到充分光顺,同时也将增大
方程条件数,使得数值性质变差.当λ过小时,光滑约束能量将占主导,此时,算法行为将与传统的投影法(如文献[12])
相似.虽然曲线得到了充分的光顺,但是距离曲面较远,投影将破坏曲线的光滑度.当λ取值适宜时,算法将兼具两类
方法的优势.图 6 展示了插值点相同但λ取值不同情况下,人脸模型上的插值曲线.

(a) 初始曲线 (b) λ=0.01 (c) λ=0.1 (d) λ=1 (e) λ=10
Fig.6 Interpolatory curves on the face model with different values of λ
图 6 λ取不同值时,人脸模型上的插值曲线