Page 299 - 《软件学报》2020年第10期

金耀 等:距离约束的网格曲面曲线设计方法 3275

较了两种方法在脚与狗头模型上所生成的闭曲线.前者算法由于采用了局部拉普拉斯光顺算法,无法处理闭合曲
线,因此所生成的曲线在首尾连接处出现尖角,而本文算法得到的曲线则在视觉上处处光滑.同时,前者算法所生成
曲线的采样点均在网格边上,无法做到自适应细分,因此其光滑度受到网格分辨率的影响,如图 9(b)、图 10(b)所示,
曲线上的“折角”较为明显.此外,在多数情况下,本文算法效率较高.对于图 9、图 10 中的 4 个例子,本文算法的运行
时间分别为 27.8、25.4、28.4 与 44.0(ms),而文献[4]算法则分别需要 123、27、68、14(ms).

(a) 文献[24]中算法设计的曲线 (b) 本文算法设计的曲线 (c) 两条曲线叠加的结果
Fig.8 Comparison results of the algorithm [24] and our method on the wings of the gargoyle model
图 8 文献[24]中算法与本文算法在怪兽翅膀模型的结果比较

(a) 瓶子模型上的开曲线 (b) 梨模型上的开曲线
[4]
Fig.9 Comarison results for open curves of the algorithm and ours
图 9 文献[4]中算法与本文算法所设计的开曲线的比较结果

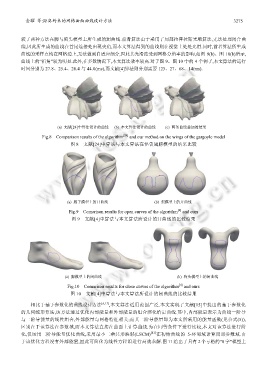
(a) 脚模型上的闭曲线 (b) 狗头模型上的闭曲线

[4]
Fig.10 Comarison results for close curves of the algorithm and ours
图 10 文献[4]中算法与本文算法所设计的闭曲线的比较结果
相比于基于参数化的曲线设计方法 [6,15] ,本文算法适用范围广泛.本文实现了文献[15]中提出的基于参数化
的几何蛇形算法,该方法通过优化内部能量和外部能量的组合演化给定曲线.其中,内部能量表示为曲线一阶导
与二阶导能量的线性组合,外部能量与网格特征相关;而其二阶导能量即为本文所采用的能量函数(见公式(5)),
区别在于该算法在参数域,而本文算法直接在曲面上计算曲线.为在同等条件下进行比较,本文对该算法进行简
化,仅运用二阶导能量优化曲线,采用最小二乘共形映射(LSCM) [41] 在初始曲线的 5-环邻域计算局部参数域.由
于该优化方程没有外部能量,因此可简化为线性方程组进行高效求解.图 11 给出了具有 2 个亏格的“8 字”模型上