Page 300 - 《软件学报》2020年第10期

3276 Journal of Software 软件学报 Vol.31, No.10, October 2020

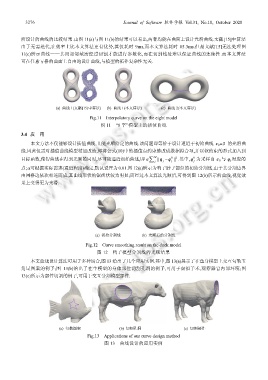
所设计的曲线的比较结果.由图 11(a)与图 11(b)的结果可以看出,两者均能在曲面上设计光滑曲线.文献[15]中算法
由于无需迭代,在效率上比本文算法更有优势,其仅耗时 9ms,而本文算法耗时 85.3ms.但是文献[15]无法处理图
11(c)所示曲线——其局部邻域需经过切割才能进行参数化,而在切割线处难以保证曲线的连续性.而本文算法
可在任意亏格的曲面上自由地设计曲线,与模型的拓扑复杂性无关.

(a) 曲线 1(文献[15]中算法) (b) 曲线 1(本文算法) (c) 曲线 2(本文算法)
Fig.11 Interpolatory curve on the eight model
图 11 “8 字”模型上的插值曲线
3.4 应 用
本文方法不仅能够设计插值曲线,且能光顺给定的曲线.该问题即等价于设计逼近于初始曲线 c 0 ∈S 的光滑曲
线.因此仅需对插值曲线模型稍加改造,即将公式(10)中的插值点约束修改成数据拟合项,并以软约束的形式加入到
目标函数,使得曲线在得到光顺的同时,尽可能逼近初始曲线,即α ∑ M || q − q 0 || .其中, q 为采样自 c 0 与 q j 对应的
2
0
j j j j
点;α可根据实际需求(逼近程度)确定,默认设置为 0.01.图 12(a)所示为鸭子脖子部位的初始分割线,由于其分割边界
由网格边依次相连而成,其曲线形状的锯齿状较为明显;而经过本文算法光顺后,可得到图 12(b)所示的曲线,视觉效
果上变得更为光滑.

(a) 初始分割线 (b) 光顺后的分割线

Fig.12 Curve smoothing result on the duck model
图 12 鸭子模型分割线的光顺结果

本文曲线设计算法可用于多种场合,图 13 给出了几个应用实例.其中,图 13(a)展示了在鱼身模型上交互勾勒五
角星图案的例子;图 13(b)给出了在牛模型的身体部位切割孔洞的例子,可用于虚拟手术,观察器官内部环境;图
13(c)所示为部件切割的例子,可用于交互分割模型部件.

(a) 勾勒图案 (b) 切割孔洞 (c) 切割部件
Fig.13 Applications of our curve design method
图 13 曲线设计的应用实例