Page 298 - 《软件学报》2020年第10期

3274 Journal of Software 软件学报 Vol.31, No.10, October 2020

由图可见:当λ取值为 1 和 10 时,曲线偏离初始曲线较近,未能得到充分光顺;当其取值为 0.1 和 0.01 时,曲线偏
离初始曲线较远,但光滑度得到了改善.为了定量比较各曲线的光滑度,本文采用表示曲线曲率的离散拉普拉斯能
量,即公式(5)进行度量.λ从 0.01 变化到 10,各曲线的光滑度分别为[0.0200,0.0133,0.0237,0.0247].通过大量实验发
现,λ=0.1 时获得的曲线能够取得较好的光滑度.因此,本文实验中将参数λ默认取作 0.1.
3.3 比较实验

相比于经典的基于能量极小化的投影法 [12] ,本文算法具有众多优点.本文实现了文献[12]中描述的算法(部分
参数原文未给出,其结果可能与原文有差异),并与本文方法进行了比较.
• 首先,本文方法效率较高.文献[12]中的方法首先松弛流形约束,然后逐步将其投影到流形上,其中,投影步
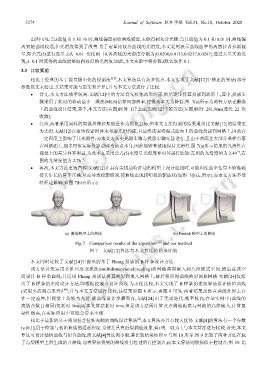
骤采用了耗时的移动最小二乘法(MLS)估算局部曲率,使得效率大为降低.图 7(a)所示为两种方法在雕像
上的曲线设计结果,其中,本文方法(右图)耗时 117.2ms,文献[12]中的方法(左图)耗时 281.9ms(迭代 22 次
收敛);
• 其次,两者采用同样的离散拉普拉斯能量作为优化目标,但本文方法得到的结果通常比文献[12]的结果更
为光滑.文献[12]在逐步投影时并未考虑光滑约束,且最终还需将隐式曲面上的曲线投影到网格上,因此在
一定程度上影响了其光滑性;而本文方法中光滑步骤与投影步骤交替进行,且由于曲面上大部分采样点落
在网格面上,很多时候实际投影点即为该点本身,因此能够有效地保持光滑性.图 7(a)所示结果的光滑性在
−6
视觉上的差异并不明显,为此本文采用公式(5)来度量光滑度并对其进行比较:左图的光滑度值为 2.49 ,右
−6
图的光滑度值为 2.76 ;
• 再次,本文方法更为鲁棒.文献[12]在具有尖锐边特征边的模型上设计曲线时,可能因法曲率估算不够准确
使其步长估算不正确,从而导致投影错误,使曲线出现较明显的锯齿状(如图 7(b)左所示),而本文方法不受
特征边影响(如图 7(b)右所示).

(a) 雕像模型上的曲线 (b) Fandisk 模型上的曲线
Fig.7 Comparison results of the algorithm [12] and our method
图 7 文献[12]算法与本文算法的结果比较

本文同时比较了文献[24]中提出的基于 Phong 投影的 B 样条设计方法.
该方法首先运用多维尺度变换法(multidimensional scaling)将网格曲面嵌入到八维欧式空间,然后在该空
间设计 B 样条曲线,并运用 Phong 投影法将其映射到嵌入网格上,最后将所得曲线映射回原网格.文献[24]仅给
出了 B 样条的正向设计方法,即根据控制点设计曲线.为方便比较,本文实现了 B 样条的逆向算法设计插值曲线
(采用夹持端点条件) [40] ,并与本文方法进行比较,其结果如图 8 所示.由图 8 可见:两者结果虽然在曲线外形上存
在一定差异,但视觉上均较为光滑.就曲线设计步骤而言,文献[24]由于无需迭代,效率较高,在该实例中(曲线的
离散点数目相同)仅耗时 1ms;而本文算法耗时 6ms.但是该方法需计算点点测地距离与网格的高维嵌入,计算复
杂性很高,在实际应用中可能会带来不便.
[4]
相比于最新的基于局部拉普拉斯光顺的曲线设计算法 ,本文算法亦具有较大优势.文献[4]的算法有一个参数
t∈(0,1],用于控制与初始曲线的逼近程度.为使其具有近似插值效果,将t统一取为1,与本文算法进行比较.首先,本文
算法可设计插值曲线与闭合曲线,而文献[4]算法则不能,其比较结果如图 9 与图 10 所示.图 9 比较了两种方法在瓶
子与梨模型上所生成的开曲线.前者算法得到的曲线没有经过所有控制点,而本文算法则能插值于控制点;图 10 比