Page 182 - 《摩擦学学报》2021年第6期

第 6 期 王大刚, 等: 微动频率对钢丝拉扭复合微动腐蚀疲劳行为影响研究 967

−20 −20 −20
−10 −10 −10
0 Tangenttial force/N 0 Tangenttial force/N 0 Tangenttial force/N
10 10 10
20 20 1 50 20
1 2 50 1 2 50 2 3 −50 0
3 4 −50 0 3 4 −50 0 Cycles/10 4 5 −100 Displacement
Cycles/10 5 −100 Displacement Cycles/10 5 −100 Displacement 4 amplitude/μm
4 amplitude/μm 4 amplitude/μm
(a) F t -D curve, f=3 Hz (b) F t -D curve, f=4 Hz (c) F t -D curve, f=5 Hz

−20 0.2
−10 0.1 0.2
0.1
0 Torque/(N·m) 0 Torque/(N·m) 0 Torque/(N·m)
10 −0.1 −0.1
20 −0.2 −0.2
1 2 2 1 2 1 2
Torsion angle/(°)
3 4 0 2 0 2 0
Cycles/10 5 −2 3 4 −2 3 4 −2
4 Cycles/10 4 5 Torsion angle/(°) Cycles/10 4 5 Torsion angle/(°)
(d) T-θ curve, f=3 Hz (e) T-θ curve, f=4 Hz (f) T-θ curve, f=5 Hz

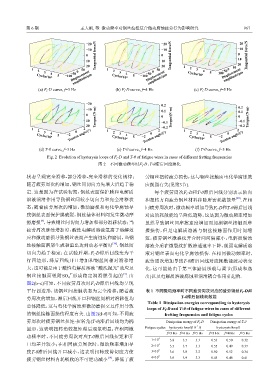
Fig. 2 Evolution of hysterysis loops of F t -D and T-θ of fatigue wires in cases of different fretting frequencies
图 2 不同微动频率时F t -D、T-θ滞后回线演化

状态呈现完全滑移-部分滑移-完全滑移的变化规律； 劳钢丝扭转疲劳损伤，这与钢丝接触面电化学腐蚀效
随着疲劳周次的增加，钢丝间切向力先增大后趋于稳 应削弱有关(见第3节).
定. 这是因为在试验初期，钢丝表面保护膜和电解质 每个疲劳周次F -D和T-θ滞后回线分别表示轴向
t
溶液润滑作用导致钢丝间较小切向力和完全滑移状 和扭转方向疲劳钢丝材料移除所需耗散能量 . 在相
[20]
态；随着疲劳周次的增加，微动磨损和电化学腐蚀导 同疲劳周次时，微动频率增加导致F -D和T-θ滞后回线
t
致钢丝表面保护膜破裂，钢丝基体材料间发生微动摩 对应的耗散能均呈降低趋势，这是因为微动频率增加
[4]
擦磨损 ，导致钢丝间切向力增加和部分滑移状态；当 虽然导致钢丝间摩擦速度增加而加剧钢丝接触面摩
疲劳周次继续增加时，酸性电解质溶液氢离子溶解效 擦损伤，但是电解质溶液与钢丝接触面作用时间缩
应和微动磨损导致钢丝表面产生腐蚀坑和磨屑，当钢 短，疲劳钢丝微裂纹开合时间间隔减小，电解质腐蚀
[18]
丝接触面磨屑生成和溢出达到动态平衡时 ，钢丝间 溶液介质在微裂纹扩散渗透速率下降，削弱电解质溶
切向力趋于稳定；在试验后期，F -D滞后回线变为平 液对钢丝表面电化学腐蚀损伤. 在相同微动频率时，
t
行四边形，滞后回线开口增加和钢丝间相对滑移增 疲劳周次增加导致T-θ滞后回线对应耗散能波动状变

大，这可能是由于酸性电解质溶液“酸洗抛光”效应及 化，这可能是由于第三体磨屑承载与调节(形成和逸
[4]
2−
钢丝接触面吸附SO 形成稳定润滑膜引起的 . 由
4 出)以及电解质溶液腐蚀和润滑耦合作用引起的.
图2(b~c)可知，不同疲劳周次时F -D滞后回线均呈现
t

平行四边形，故钢丝间接触状态为完全滑移；随着疲 表 1 不同微动频率时不同疲劳周次对应的疲劳钢丝F t -D和
劳周次的增加，滞后回线开口和钢丝间相对滑移值均 T-θ滞后回线耗散能
Table 1 Dissipation energies corresponding to hysterysis
总体降低，这与电化学腐蚀和微动磨损交互作用导致
loops of F t -D and T-θ of fatigue wires in cases of different
的钢丝接触面损伤程度有关. 由图2(d~f)可知，不同疲 fretting frequencies and fatigue cycles
劳周次时疲劳钢丝扭矩-扭转角(T-θ)滞后回线均为椭 Dissipation energy of F t -D Dissipation energy of T-θ
−3 hysterysis loop/J
Fatigue cycles hysterysis loop/(10 J)
圆形，这表明扭转角较扭矩滞后现象明显；在相同微
f=3 Hz f=4 Hz f=5 Hz f=3 Hz f=4 Hz f=5 Hz
动频率时，不同疲劳周次对应T-θ滞后回线扭矩和开
1×10 4 3.8 3.5 3.3 0.53 0.50 0.32
口均差异较小；在相同疲劳周次时，微动频率增加导 2×10 4 3.5 3.7 3.3 0.55 0.49 0.37
致T-θ滞后回线开口减小，这表明扭转致剪切应力使 3×10 4 3.6 3.8 3.2 0.50 0.52 0.34
4
4×10
[19]
疲劳钢丝材料内耗吸收的不可逆功减小 ，降低了疲 3.9 3.9 3.3 0.45 0.48 0.41