Page 205 - 《振动工程学报》2025年第9期

第 9 期 刘志军，等：基于 AVME-OMOMEDA 的滚动轴承复合故障诊断 2135

2 2 4

幅值 0 幅值 0 2
−2 −2 幅值 0
0 0.2 0.4 0.6 0.8 1.0 0 0.2 0.4 0.6 0.8 1.0 −2
时间 / s 时间 / s −4
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
(a) 内圈故障信号 (b) 外圈故障信号 时间 / s
(a) Inner ring fault signal (b) Outer ring fault signal (a) 时域图
(a) Time-domain diagram
2 2
幅值 0 幅值 0 0.4 65 Hz
−2 −2 0.3 97 Hz
0 0.2 0.4 0.6 0.8 1.0 0 0.2 0.4 0.6 0.8 1.0 幅值 0.2
时间 / s 时间 / s 0.1
(c) 谐波干扰信号 (d) 随机冲击信号 0
(c) Harmonic interference signal (d) Random impulse signal 0 50 100 150 200 250 300 350 400 450 500
频率 / Hz
5 (b) 包络谱
幅值 −5 0 (b) Envelope spectrum
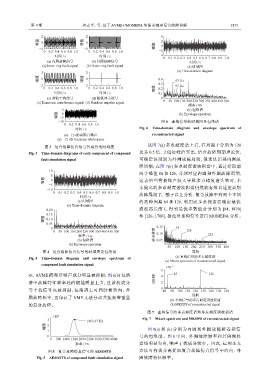
−10 图 6 重构信号的时域图及包络谱
0 0.2 0.4 0.6 0.8 1.0
时间 / s Fig. 6 Time-domain diagram and envelope spectrum of
(e) −15 dB高斯白噪声 reconstructed signal
(e) −15 dB Gaussian white noise

从图 7(a) 多点峭度谱上看，在周期 T 分别为 126
图 3 复合故障仿真信号各成分的时域图
Fig. 3 Time-domain diagrams of each component of compound 及其 0.5 倍、2 倍处峰值突出，结合故障周期理论值，
fault simulation signal 可确定该周期为外圈故障周期，但无法识别内圈故
障周期；在图 7(b) 多点峭度谐波积谱中，通过拾取前

10 两个峰值 和 126，分别对应内圈和外圈故障周期，
5 84
幅值 0 这表明当背景噪声较大导致多点峭度谱失效时，本
−5
−10 文提出的多点峭度谐波积谱仍然能有效自适应识别
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 故障周期 T。基于以上分析，复合故障中有两个不同
时间 / s
(a) 时域图 的故障周期 84 和 126，利用定步长搜索法确定最优
(a) Time-domain diagram
0.20 滤波器长度 L，得到最优参数组合分别为 [84，1870]
幅值 0.15 和 [126，1760]，据此对重构信号进行 MOMEDA 分析。
0.10
0.05
0 63
0 50 100 150 200 250 300 350 400 450 500 多点峭度 0.15 126
0.10
频率 / Hz 252
(b) 包络谱 0.05
(b) Envelope spectrum
50 100 150 200 250 300 350 400
图 4 复合故障仿真信号的时域图及包络谱 周期
(a) 重构信号的多点峭度谱
Fig. 4 Time-domain diagram and envelope spectrum of
(a) Mkurt spectrum of reconstructed signal
compound fault simulation signal
×10 −7
6
示，AVME 降噪后噪声成分明显被抑制；图 6(b) 包络 4 84 126
谱中故障特征频率处的幅值明显上升，且谐波成分 MKHP 2
等干扰信号也被抑制，包络谱上可同时看到内、外 0 80 90 100 110 120 130 140 150 160
周期
圈故障频率，这印证了 VME 无法分离共振频带重叠
(b) 重构信号的多点峭度谐波积谱
的复合故障。 (b) MKHPS of reconstructed signal

图 7 重构信号的多点峭度谱和多点峭度谐波积谱

×10 8
3 1463.67 Hz Fig. 7 Mkurt spectrum and MKHPS of reconstructed signal
幅值 2 1 图 8(a) 和 (b) 分别为内圈和外圈故障解卷积信

0 号的包络谱。图 8 中内、外圈故障频率和其倍频处
0 500 1000 1500 2000 2500 3000 3500 4000
频率 / Hz 谱线明显突出，噪声干扰成分较少。因此，运用本文

图 5 复合故障仿真信号的 AESOSTS 方法可有效分离提取复合故障仿真信号中的内、外
Fig. 5 AESOSTS of compound fault simulation signal 圈故障特征频率。