Page 180 - 《振动工程学报》2025年第9期

2110 振 动 工 程 学 报 第 38 卷

式中，Δt 为采样时间间隔，且： 件下，图 5 中斜率为 2 的线即为高、低压转子的共同
( ) Z ia,t −Z ib,t−∆t 工作线，其与高/低压激振共振转速线的交点即为
f Z ia,t −Z ib,t−∆t =

高/低压激振的临界转速。在给定参数条件下，高/低
Z ia,t −Z ib,t−∆t
需要注意的是，不包含轴承座自由度时，AMDFD 压激振的第 1、2 阶临界转速为 885/1857 r/min、1255/
静摩擦片是静止的，因此 a 点的位移是动摩擦片的 2503 r/min，对应振型如图 6 所示。由于高、低压转子
绝对位移。当考虑轴承座自由度时，静摩擦片的位 激振的对应阶次的临界转速振型基本相同，因此为
移就是对应轴承座自由度的位移，此时 a 点的位移 节约篇幅，图 6 仅列出低压激振的临界转速振型。
为动摩擦片的绝对位移与静摩擦片的位移之差。

1.3 轴向电磁执行器模型

0.2
根据式 (11)，摩擦副产生的摩擦力与所受的正压
Y 0
力 N i, 有关。所设计的 AMDFD 使用电磁铁作为控制 1.5
t
−0.2
摩擦副正压力的执行器，根据文献 [16]，可以得到电 1.0
0.2 0.5
磁执行器所产生的正压力为： 0 转子轴线 / m
X −0.2 0
2 2
µ 0 A 0 N i
N i,t = 0 c （12） (a) 1阶临界转速处振型
4s 2
0 (a) Mode shape at the first critical speed
式 中， μ 0 为 真 空 磁 导 率 ； A 0 为 电 磁 铁 的 磁 极 面 积 ；
N 0 为电磁执行器的线圈匝数；s 0 为图 1 中电磁铁和
0.4
推力盘之间的轴向气隙；i c 为电磁执行器的控制电
流。可见，当电磁执行器结构确定后，电磁执行器的 Y 0
电磁力与控制电流 i c 的平方成正比。 −0.4 1.5

0.4 1.0
0 0.5
2 双 转 子 系 统 的 动 力 特 性 X −0.4 0 转子轴线 / m
(b) 2阶临界转速处振型
(b) Mode shape at the second critical speed
为了更好地抑制双转子系统过临界转速时的外
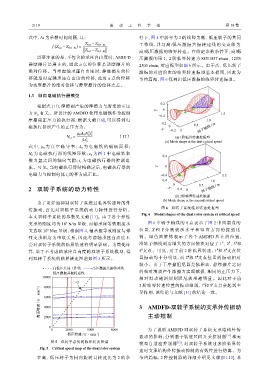
传振动，首先对双转子系统的动力特性进行分析。 图 6 双转子系统临界转速处振型
Fig. 6 Modal shapes of the dual rotor system at critical speed
本文双转子系统的参数见文献 [11]。由于各个弹性
6
支承的刚度均为 10 N/m 量级，而轴承座等效刚度本 图 6 中转子轴线的 0 点表示了图 2 中风扇盘的
文选取 10 N/m 量级，根据图 4，轴承座等效刚度与弹 位 置， X 和 Y 分 别 表 示 水 平 和 竖 直 方 向 的 振 型 比
8
性支承刚度为串联关系，因此考虑轴承座自由度不 例 。 绿 色 圆 锥 体 表 示 了 各个 AMDFD 所 在 的 位 置 ，
#
#
#
会对双转子系统的临界转速有明显影响。为简化计 沿转子轴线刻度增大的方向依次对应了 1 、2 、3 和
#
#
算，基于不考虑轴承座自由度的双转子系统模型，得 5 支点。可见，对于前 2 阶临界转速，1 和 # 5 支点位
#
到双转子系统的临界转速图谱如图 5 所示。 置振动均十分明显，而 2 和 # 3 支点位置的振动相对
较小。由于干摩擦阻尼器是依靠动、静摩擦片之间

高低压共同工作线 高压激振共振转速线
低压激振共振转速线 的相对滑动产生摩擦力实现减振，相同的正压力下，
10000 相对滑动越剧烈则阻尼效果越明显。因此对于前
×2
5 支点会起到主
#
阶临界转速位置的振动抑制，1 和
#
2 导作用，该结论与文献 [11] 的结论一致。
8000
高压转速 / (r·min −1 ) 6000 3 AMDFD-双 转 子 系 统 的 支 承 外 传 振 动

4000
2000
0 主 动 控 制
0 2000 5000 8000 为了说明 AMDFD 对双转子系统支承结构外传
−1
低压转速 / (r·min )
振动的影响，分别基于转速区间开关控制器 [11] 和无

图 5 双转子系统的临界转速图谱 [12]
模型自适应控制器 ，对双转子系统过多阶临界转
Fig. 5 Critical speed map of the dual rotor system
速时支承结构外传振动抑制的有效性进行仿真。为
在高、低压转子为同向旋转且转速比为 2 的条 节约篇幅，2 种控制器的详细介绍见文献 [11-12]，本