Page 235 - 《软件学报》2025年第9期

4146 软件学报 2025 年第 36 卷第 9 期

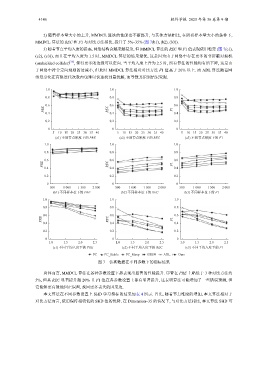
2) 随着样本量大小的上升, MMDCL 算法的性能也不断提升, 与其他方法相比, 在所有样本量大小的条件下,
MMDCL 算法的 REC 和 F1 与对比方法相比, 提升了 5%–35% (图 7(b1), (b2), (b3)).
3) 随着节点平均入度的提高, 网络结构会越来越复杂, 但 MMDCL 算法的 REC 和 F1 值表现依旧稳定 (图 7(c1),
(c2), (c3)), 而且在平均入度为 1.5 时, MMDCL 算法的结果最优, 这是因为由于网络中存在更多的非屏蔽对撞机
[33]
(unshielded collider) , 使得更多的边缘可以定向. 当平均入度上升为 2.5 时, 所有算法的性能均有所下降, 这是由
于网络中符合定向规则的边减小, 但此时 MMDCL 算法相对对比方法 F1 值高于 20% 以上. 而 ADL 算法随着网
络复杂化在有限迭代次数内也难以快速找到最优解, 而导致其识别结果受限.

1.0 1.0 1.0
0.8 0.8 0.8
0.6 0.6 0.6
PRE REC F1
0.4 0.4 0.4
0.2 0.2 0.2
0 0 0
5 10 15 20 25 30 35 40 5 10 15 20 25 30 35 40 5 10 15 20 25 30 35 40
(a1) 不同节点维度下的 PRE (a2) 不同节点维度下的 REC (a3) 不同节点维度下的 F1
1.0 1.0 1.0
0.8 0.8 0.8
0.6 0.6 0.6
PRE REC F1
0.4 0.4 0.4
0.2 0.2 0.2
0 0 0
500 1 000 1 500 2 000 500 1 000 1 500 2 000 500 1 000 1 500 2 000
(b1) 不同样本量下的 PRE (b2) 不同样本量下的 REC (b3) 不同样本量下的 F1
1.0 1.0 1.0
0.8 0.8 0.8
0.6 0.6 0.6
PRE REC F1
0.4 0.4 0.4

0.2 0.2 0.2
0 0 0
1.0 1.5 2.0 2.5 1.0 1.5 2.0 2.5 1.0 1.5 2.0 2.5
(c1) 不同平均入度下的 PRE (c2) 不同平均入度下的 REC (c3) 不同平均入度下的 F1
PC PC_Stable PC_Maxp GSBN ADL Ours
图 7 仿真数据在不同参数下的指标结果

总体而言, MMDCL 算法在各种参数设置下都表现出显著的性能提升. 尽管在 PRE 上略低于 3 种对比方法约
5%, 但其 REC 显著提升超 20% 且 F1 值在各参数设置上都有显著提升, 这表明算法可能增加了一些错误预测, 但
它能够更有效地纠正误判, 找回更多丢失的因果边.
本文算法在不同参数设置上 SHD 学习指标的结果如表 4 所示. 首先, 随着节点维度的增加, 本文算法相对于
对比方法而言, 依旧保持相较低的 SHD 值的优势. 在 Dimension=35 的情况下, 与对比方法相比, 本文算法 SHD 可