Page 230 - 《软件学报》2025年第9期

郝志峰 等: 基于增强条件独立性检验的鲁棒因果发现算法 4141

3.1 增强条件独立性检验的领域搜索

在邻域搜索阶段, 算法的核心任务是从当前得到的部分有向无环图 G pd 出发, 搜索下一步可能候选结构. 考虑
到在当前结构中可能存在部分节点的因果边因 CIT 的错误判断而被误删的问题, 因此, 本阶段对当前结构中所有
非邻接节点进行二次、增强的 CIT 检验来重新评估它们之间的因果关系, 从而有效识别并恢复节点间被误删的因
果边.
为了最大可能地找回被误删的因果边, 算法将候选的搜索空间设置为当前结构中所有非邻接节点之间的潜在
因果边, 并通过结构先验信息消除待检验节点存在的外部父节点影响, 进行二次检验判断当前节点之间的因果关
系是否可以被其邻居节点 d-分离. 本文形式化该过程为增强条件独立性检验, 如定义 4 所示.
定义 4. 增强的条件独立性检验. 数据集 D 表示因果图结构 G = {V,E} 的节点和边的集合, 其中图的节点对应
pd
数据中的观测变量, 即 V i 表示 . 在当前的结构 G pd 上, 对于任意节点 V i ∈ V 的非邻接节点 V j ∈ Ad j(G,V i ) 表示为
X i
( )
V i ,V j , 关于 V i ,V j 的增强条件独立性检验定义如下:

)
(
(
)
ˆ V i ⊥ ˆ V j |dSet V i ,V j ∥ ˆ V i ⊥ ˆ V j |dSet V i ,V j ∪S,
V i V j 在当前结构中排
;
其中, 对 V i 和 V j 分别回归图 G pd 中已知的父节点得到 ˆ V i 和 ˆ V j S 是 Nei 的非空子集, Nei 表示 ,
pd pd pd
除了已经过回归处理的节点后的邻接节点集合, 公式表示为 S ⊆ Nei,Nei = {(Ad j(G ,V i )∨ Ad j(G ,V j ))−(Pa(G ,V i )∨
pd ˆ V j 表示为公式 (3):
Pa(G ,V j ))}}, 其中 ˆ V i 和

∑
∑
ˆ
ˆ V i = V i − b ik V k , V j = V j − b ik V k (3)
V k ∈Pa( G pd ,V i) V k ∈Pa( G pd ,V j)
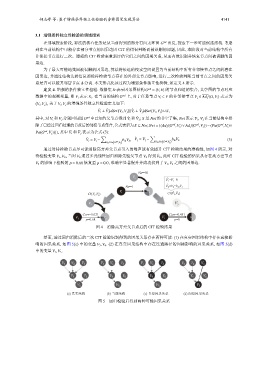
通过对待检验节点尽可能消除高方差父节点引入的噪声能有效提升 CIT 检验结果的准确性, 如图 4 所示, 对
ˆ V 2 , 此时 CIT 检验的结果从存在高方差节点
待检验变量 V 1 ,V 2 , 当对 V 2 通过多元线性回归消除先验父节点 V 3 得到
V 3 的影响下检验的 p = 0.68 恢复至 p = 0.0, 准确率显著提升并成功找到了 V 1 ,V 2 之间的因果边.

Var=50
V 3
V 1 =V 1 −0
Var=1 V 2 =V 2 −b 13 V 3
V 1 V 2
CI(V 1 ,V 2 ) CI(V 1 ,V 2 )
V 3 V 3
Corr=0.021 Corr=0.451
V 1 V 2 V 1 V 2
p=0.68 p=0
图 4 消除高方差父节点后的 CIT 检验结果

然而, 通过回归消除后的二次 CIT 检验识别得到的因果关系存在两种可能: (1) 在真实因果结构中存在直接影
响的因果关系, 如图 5(c) 中的变量 V 3 ,V 4 . (2) 在真实因果结构中存在连通路径的间接影响的因果关系, 如图 5(d)
V 3 ,V 5 .
中的变量

(a) 真实结构 (b) 当前结构 (c) 直接因果关系 (d) 间接因果关系
图 5 回归检验后得到两种可能因果关系