Page 191 - 《软件学报》2025年第9期
P. 191
4102 软件学报 2025 年第 36 卷第 9 期
Λ t = 1−(1−Λ 1 )ν t−1 (15)
[ ]
T
P t = E ˜w t ˜w α 2 t (16)
t
0.8 0.8
0.7 MTP (1 024) 0.7 MTP (1 024)
MTP (ours)
能量 RMSE (eV) 0.5 力 RMSE (eV/Angstrom) 0.5
0.6
MTP (ours)
0.6
0.4
0.4
0.3
0.3
0.2
0.1 0.2
0.1
0 0
−0.1 −0.1
Cu Au Al C Li Mg S Si H 2 O CuC NaCl Cu Au Al C Li Mg S Si H 2 O CuC NaCl
(a) 能量 (b) 原子受力
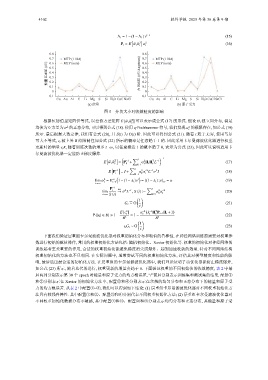
图 5 分块大小对收敛精度的影响
[ T ]
根据伍德伯里矩阵恒等式, 误差协方差矩阵 E ˜w t ˜w 可以表示成公式 (17) 的形式. 假设 H i 独立同分布, 满足
t
均值为 0 方差为 σ 的正态分布, 可以得到公式 (18). 使用 q-Pochhammer 符号, 我们发现 α 的极限存在, 如公式 (19)
2
2
t
所示. 最后根据大数定律, 我们有公式 (20), 且 S(t) 为 O(t) 阶. 因此可以得到公式 (21). 随着 t 趋于无穷, 使用马尔
可夫不等式, ϵ t 被上界 B 给限制住如公式 (22) 所示的概率是任意趋于 1 的. 因此采用卡尔曼滤波优化器进行权重
更新时的增量 ϵ t K t 随着训练次数的增多 t– ∞, 以任意接近 1 的概率趋于 0, 表示为公式 (23), 因此可以说明适用卡
尔曼滤波优化器一定能防止梯度爆炸.
( ) −1
[ ] ∑ t
2
T
−1
T
E ˜w t ˜w = P + α H i H L −1 (17)
t 0 i i
i=1
[ ] ∑ t
2
2
−2
−1
E P −1 = I + α α L σ I (18)
t k=1 k t
( )
i
2
lim α = Π ∞ 1−(1−λ 1 )ν = ((1−λ 1 );ν) ∞ = α (19)
t i=0
t→∞
P −1 a.s. ∑ t
2
−1
2
lim t → σ L , S (t) := α α −2 (20)
t→∞ S (t) k=1 k t
( )
a.s. 1
G t ∼ O (21)
t
[ ]
T
E ϵ t 2 α −2 ( λ H P t−1 H t +1 )
−1
t
t
t
P(|ϵ t | ⩽ B) ⩾ 1− = 1− (22)
B 2 B 2
( )
1
ϵ t G t ∼ O (23)
t
下面我们验证层重组卡尔曼滤波优化器对权重初始化分布和取值的鲁棒性. 在神经网络训练前需要对权重参
数进行初始的赋值操作, 常用的权重初始化方法包括: 随机初始化、Xavier 初始化等. 权重的初始化对神经网络的
训练起着至关重要的作用, 合适的权重初始化能避免梯度消失或爆炸、起到加速收敛的效果. 针对不同网络结构
权重初始化的方法也不尽相同. 在实际问题中, 通常尝试不同的权重初始化方法, 评估其对模型精度和性能的影
响, 最后选出最合适的初始化方法. 在层重组的卡尔曼滤波优化器中, 我们理论证明了该优化器能防止梯度爆炸,
如公式 (23) 所示, 随着迭代的进行, 权重更新的增量会趋于 0. 下面验证权重的不同初始值的收敛精度, 表 2 中最
后两列分别表示第 30 个 epoch 时能量和原子受力的均方根误差, “/”前后分别表示训练集和测试集的结果. 配置①
和②分别表示在 Xavier 的初始化方法中, 配置③和④分别表示在常规的均匀分布和正态分布下的能量和原子受
力的均方根误差. 从表 2 中配置①–④, 我们可以得到如下结论: (1) 层重组卡尔曼滤波优化器对不同权重初始化方
法具有较强鲁棒性. 其中配置①和②、配置③和④分别代表不同权重初始化方法; (2) 层重组卡尔曼滤波优化器对
不同权重初始化数据分布不敏感, 其中配置①和③、配置②和④分别表示均匀分布和正态分布, 其能量和原子受