Page 195 - 《软件学报》2025年第9期

4106 软件学报 2025 年第 36 卷第 9 期

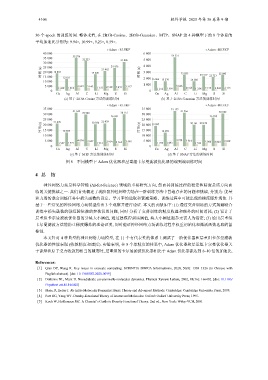
30 个 epoch 的训练时间. 整体来看, 在 2B3B-Cosine、2B3B-Gaussian、MTP、SNAP 这 4 种模型下的 8 个体系的
平均加速比分别为: 9.94×, 10.99×, 9.25×, 8.59×.

Adam RLEKF Adam RLEKF
40 000 6 000
35 576 54 221
35 000 32 523 31 086 5 000
30 000 24 456 4 000
时间 (s) 25 000 18 862 17 849 21 462 时间 (s) 3 000 25 885 23 317 22 323 25 843
20 000
15 000
10 000 12 831 2 000 16 066 15 279 15 380
1 000
5 000 3 639 3 142 3 217 5 826
1 458 1 618 1 731 2 518 2 431 1 152 1 399 25 68 1 258 2 135 2 026 2 715
0 0
Cu Ag Al C Li Mg S Si Cu Ag Al C Li Mg S Si
(a) 基于 2B3B-Cosine 方法的训练时间 (b) 基于 2B3B-Gaussian 方法的训练时间
Adam RLEKF Adam RLEKF
35 000 35 000 33 137
31 633 31 566 30 882
30 000 29 948 30 115 30 000
26 681 26 920
25 000 21 476 20 596 21 459 25 000 20 161 20 132
时间 (s) 20 000 12 845 时间 (s) 20 000 19 097 12 859
15 000
15 000
10 000 10 000
5 000 4 024 3 687 2 934 3 448 5 000 4 279 3 816 3 094 2 863 3 638
1 587 1 771 1 913 2 563 1 735 1 893 1 913
0 0
Cu Ag Al C Li Mg S Si Cu Ag Al C Li Mg S Si
(c) 基于 MTP 方法的训练时间 (d) 基于 SNAP 方法的训练时间
图 6 不同模型下 Adam 优化器和层重组卡尔曼滤波优化器的端到端训练时间

4 总 结

神经网络力场是科学智能 (AI-for-Science) 领域的重要研究方向, 然而其训练过程的稳定和精度是该方向面
临的关键挑战之一. 我们首先概述了现阶段神经网络力场在一阶训练方法中普遍存在的问题和挑战, 分别为: 能量
和力场的联合训练任务中损失函数的设定、学习率的选取和衰减策略、训练过程中可能出现的梯度爆炸现象. 并
基于一些常见的神经网络力场模型给出 3 个观察并进行论证. 本文的贡献如下: (1) 通过交替训练的方式规避联合
训练中损失函数的强经验依赖的参数设置问题, 同时 分析了交替训练的精度收益和额外的时间消耗; (2) 设计了
层重组卡尔曼滤波优化器的分块大小阈值, 通过建模得到该阈值, 块大小阈值超参无需人为指定; (3) 给出层重组
卡尔曼滤波方法能防止梯度爆炸的理论证明, 同时验证神经网络力场训练过程中权重初始化和激活函数选取的鲁
棒性.
本文针对 4 种典型的神经网络力场模型, 在 11 个有代表性的体系上测试了一阶优化器和层重组卡尔曼滤波
优化器的性能表现 (收敛精度和速度). 实验表明, 在 8 个单精度的体系中, Adam 优化器和层重组卡尔曼优化器关
于能量和原子受力收敛到相当的精度时, 层重组的卡尔曼滤波优化器相比于 Adam 优化器能达到 8–10 倍的加速比.

References:
[1] Qian DP, Wang R. Key issues in exascale computing. SCIENTIA SINICA Informationis, 2020, 50(9): 1303–1326 (in Chinese with
English abstract). [doi: 10.1360/SSI-2020-0099]
[2] Doltsinis NL, Marx D. Nonadiabatic car-parrinello molecular dynamics. Physical Review Letters, 2002, 88(16): 166402. [doi: 10.1103/
PhysRevLett.88.166402]
[3] Marx D, Hutter J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods. Cambridge: Cambridge University Press, 2009.
[4] Parr RG, Yang WT. Density-functional Theory of Atoms and Molecules. Oxford: Oxford University Press, 1995.
[5] Koch W, Holthausen MC. A Chemist’s Guide to Density Functional Theory. 2nd ed., New York: Wiley-VCH, 2001.