Page 188 - 《软件学报》2025年第9期

胡思宇 等: 基于层重组扩展卡尔曼滤波的神经网络力场训练 4099

根据表 1 可知, 模型收敛精度随着 α和β 取值的不同会发生改变, 其中配置④随着迭代次数动态变动的方案在
典型的铜数据集上, 基于 Adam 优化器的训练下, 具有最低的误差. 其他权重系数配置, 在测试集的能量预测效果
上, 比配置④差 10.26%–29.52% 不等, 平均差 20.64%. 在测试集的原子受力的预测上, 比配置④差 1.23% 到
97.81% 不等, 平均差 44.68%. 不同权重系数配置的 RMSE 几乎在同一量级, 但由于神经网络力场模型对能量和原
子受力的精度要求极高 (神经网络力场模型的训练数据为高精度的 DFT 数据), RMSE 在绝对值上相差微小, 但百
α和β 的取值, 高度依赖
分比差异显著. 总的来说, 这种联合训练存在两个问题: (1) 对于配置①–⑤中列举的有限的
经验, 且无法保证所选的权重因子已经是最优的; (2) 当更多的预测目标加入时, 比如维里系数、磁矩等, 又会涉及
新的预测目标的平方误差的权重取值问题. 三目标函数的权重损失系数取值包含 3 个自由度, 四目标函数的权重
损失系数取值为 3 个自由度, 随着预测目标的增加, 损失因子 (pre-factor) 的组合数更多.
● 观察 2: 一阶优化器往往结合学习率一起用于神经网络的权重更新, 学习率的初始值及衰减策略影响最终收
敛结果.
随着神经网络的发展, 训练方法及优化器也在快速发展. 在随机梯度下降的一阶优化器基础上, 近年来产生很
多变体, 例如引入动量的方法. 在实际的训练任务中, 优化器的时候通常还会辅助以初始的学习率以及迭代过程中
学习率的特定改变策略来达到预期的训练效果. 神经网络力场模型的训练过程中依然存在很多的关于学习率的选
取的问题, 暂时没有达成一致的共识应该如何确定学习率的选取和改变. 例如在 Huang 等人 [36] 的工作中, 学习率
的初始值选取为 0.000 1. 而在 DeePMD 模型中, 默认的初始学习率为 0.001, 且每 5 000 个迭代步按 0.95 指数衰减.
我们发现: (1) 采用衰减的学习率比固定学习率, 得到的收敛结果精度更高; 例如铜体系下, 固定初始学习率分别
为 0.1、0.001、0.000 1 时训练集收敛到 1 000 个 epoch 时的能量和原子受力的均方误差分别为 (12.521, 0.760)、
(0.194, 0.061 3)、(0.166, 0.063 3). (2) 不同初始学习率对精度的影响大. 以深度势能模型为例, 当训练 batchsize 为
1 时, 初始学习率为 0.001 时, 学习率按 0.95 指数衰减情况下, CuO 体系的能量 RMSE 可收敛到 0.063 8 eV. 当训
练 batchsize 增加到 32 时, 初始学习率缩放根号 32 倍时, CuO 体系的 RMSE 无法降至 0.063 8 eV. 这表明初始学习
率设置不当易引发训练的不稳定现象.
● 观察 3: 一阶优化器在训练过程中会由于优化器选择不当导致梯度爆炸.
梯度消失和爆炸是神经网络训练过程中经常遇到的现象, 而现有的解决梯度消失或爆炸问题一般从网络、损
失函数、激活函数等方面找原因. 一种常用的规避梯度爆炸现象的手段是在训练过程中对每次迭代更新的权重做
一个截断, 限制更新幅度. 这种方法会引入额外的幅度超参数并一定程度上可能限制神经网络的快速收敛. 在我们
的调研中, 发现一阶优化器本身无法防止梯度爆炸的问题. 在神经网络力场模型中, 优化器的选取显得更为敏感,
不当的优化器会引发梯度爆炸的现象. 例如以 DeePMD 为例, 我们发现在 Adam 优化器的训练下能有效收敛的铜
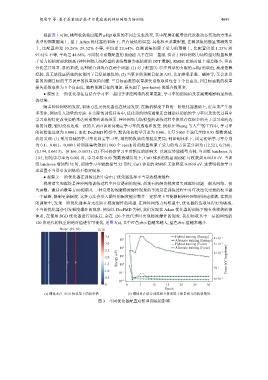
体系, 在使用 SGD 优化器进行训练后, 会在 120 个迭代步时出现梯度爆炸的现象. 我们抽取其中一层的网络的
120 次迭代的权重的绝对值进行可视化, 见图 3(a), 其中红色表示值越来越大, 蓝色表示值越来越小.

Shape: (25, 50) 1E16
3.5 Hybrid training (Energy) 4×10 −1
10 3 Alternate training (Energy)
3.0 Hybrid training (Force) 3×10 −1
10 2 Alternate training (Force)
2.5 2×10 −1
Energy (eV) Force (eV/Angstrom)
2.0 10 1
1.5 10 0
10 −1
1.0
10 −1
0.5 6×10 −2
10 −2
0 0 5 10 15 20 25 30
Epoch
(a) 铜体系在 SGD 优化器下的权重值 (b) 铜体系在联合训练和交替训练下能量和力的收敛情况
图 3 不同优化器配置对模型训练的影响