Page 344 - 《软件学报》2025年第7期

曹艺 等: 融合扩增技术的无监督域适应方法 3265

于度量的算法, 例如 DAN 和 JAN, 通过最小化源域与目标域之间的距离获得域共享特征, 进而实现域适应效果.
但此类方法忽略了目标域数据的分类信息, 本文提出的 A-UDA 算法使用阈值筛选的伪标签技术减少目标域伪标
签的分类不确定性, 从而降低使用错误标注的样本在迭代学习过程中所带来的负面影响, 间接实现增加带有正确
标注的训练数据的效果, 同时利用一致性正则化技术提高模型的泛化性能.
在表 4 和表 5 中, A-UDA 方法在 ImageCLEF-DA 数据集中 I→P 任务、I→C 任务以及 Office-Home 数据集
中 A-P 任务上均稍逊于 CDAN+E 方法取得的最佳结果, 但与最佳结果的准确率较为接近. 其原因是 CDAN+E 方
法采用了条件生成对抗网络生成域适应任务中的训练样本, 其样本生成过程考虑了类别信息和样本特征之间的联
合分布. 而本文通过添加伪标签的方式为分类器学习添加类别分布信息, 在保证准确率的同时, 显著减少了深度模
型迭代训练过程中所需要的时间和空间代价. 另外, 通过 CDAN 方法、CDAN+E 方法和 A-UDA 方法与其他方法
的实验结果比较可以看出, 同时考虑类别信息与样本的特征学习无监督域适应任务上的分类器, 可以获得更高的
准确率和更好的性能.
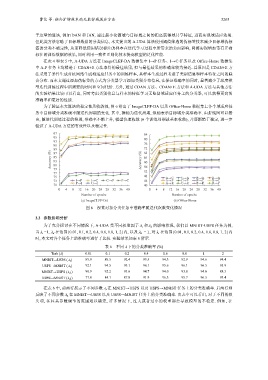
为了验证本文算法的稳定性及收敛性, 图 6 给出了 ImageCLEF-DA 以及 Office-Home 数据集上各个域适应任
务中目标域分类准确率随迭代周期的变化. 其中, 横轴为迭代周期, 纵轴表示目标域分类准确率. 由折线图可以看
出, 随迭代训练过程的推进, 准确率不断上升, 模型快速收敛 (6 个训练周期就基本收敛), 并逐渐趋于稳定, 进一步
验证了 A-UDA 方法的有效性以及稳定性.

97 84
95 80
93
91 76
89 72
Accuracy (%) 85 Accuracy (%) 64
68
87
83
60
81
79 56
52
77
75 48 A→C C→A P→A R→A
73 I→P I→C C→P P→C 44 A→P C→P P→C R→C
P→R
R→P
P→I
A→R
C→I
C→R
71 40
0 4 8 12 16 20 24 28 32 36 40 0 4 8 12 16 20 24 28 32 36 40
Number of epochs Number of epochs
(a) ImageCLEF-DA (b) Office-Home
图 6 视觉对象分类任务中准确率随迭代次数变化情况

3.3 参数影响分析
为了充分探讨在不同情况下, A-UDA 受不同权重因子 λ t 和 λ d 的影响状况, 我们以 MNIST-USPS 任务为例,

当 λ t =1, λ d 在范围{0.01, 0.1, 0.2, 0.4, 0.6, 0.8, 1, 2}内, 以及 λ d = 1, 对 λ t 在范围{0.01, 0.1, 0.2, 0.4, 0.6, 0.8, 1, 2}内
时, 本文对各个任务上的准确率进行了比较. 实验结果如表 6 所示.

表 6 不同 λ 下的分类准确率 (%)

Task (λ) 0.01 0.1 0.2 0.4 0.6 0.8 1 2
MNIST→USPS ( λ t ) 85.9 89.5 92.4 93.5 94.3 92.9 94.6 94.4
USPS→MNIST ( λ t ) 92.1 94.5 95.1 96.1 95.6 96.1 96.5 95.9
MNIST→USPS ( λ d ) 90.9 92.2 93.6 94.7 94.0 93.8 94.6 88.3
USPS→MNIST ( λ d ) 77.0 84.1 87.0 91.9 96.3 95.7 96.5 93.4

在表 6 中, 前两行展示了不同参数 λ t 在 MNIST→USPS 以及 USPS→MNIST 任务上的分类准确率. 后两行则

反映了不同参数 λ d 在 MNIST→USPS 以及 USPS→MNIST 任务上的分类准确率. 由表中可以看出, 对于不同的损
失项, 往往其参数调节的范围难以确定, 许多情况下, 过大或者过小的权重都会导致模型的不稳定. 例如, 在