Page 495 - 《软件学报》2025年第5期

朱鹏程 等: 面向分布式超导量子计算架构的量子线路映射 2395

含的 CNOT 门数; 第 5–10 列分别给出了两种算法在各基准线路上的运行结果, 包括插入的 SWAP 门数 (#SWAP)、
ST 门数 (#ST) 以及以 s 为单位的运行时间 (time); 最后两列分别给出了 DQM 算法在 SWAP 门和 ST 门上相较
DQP 算法的减少幅度. 如表 2 所示, DQM 在 SWAP 门数和 ST 门数上远优于 DQP, 在所有基准线路上, DQM 所需
的 SWAP 门较 DQP 最多减少 89.39%, 平均减少 69.69%; 类似的, DQM 所需的 ST 门最多减少 94.59%, 平均减少
85.88%.

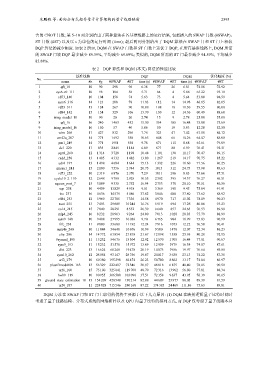
表 2 DQP 算法和 DQM (本文) 算法的性能比较

基准线路 DQP DQM 优化幅度 (%)
No.
name #n #g #SWAP #ST time (s) #SWAP #ST time (s) #SWAP #ST
1 qft_10 10 90 298 96 6.38 77 26 6.81 74.16 72.92
2 sys6-v0_111 10 98 184 58 5.71 64 4 5.88 65.22 93.10
3 rd73_140 10 104 158 74 5.63 73 4 5.64 53.80 94.59
4 sym6_316 14 123 208 78 11.93 112 14 14.98 46.15 82.05
5 rd53_311 13 124 267 90 10.88 108 18 11.30 59.55 80.00
6 rd84_142 15 154 329 106 13.70 130 12 14.36 60.49 88.68
7 ising_model_10 10 90 20 20 2.74 15 9 2.78 25.00 55.00
8 qft_16 16 240 1 463 432 15.30 354 105 16.48 75.80 75.69
9 ising_model_16 16 150 57 40 5.86 50 19 5.03 12.28 52.50
10 wim_266 11 427 832 296 7.76 323 47 7.42 61.18 84.12
11 cm42a_207 14 771 1 692 550 10.65 608 66 10.26 64.07 88.00
12 pm1_249 14 771 1951 550 9.78 671 115 8.68 65.61 79.09
13 dc1_220 11 833 2 845 1 144 6.89 671 88 6.99 76.41 92.31
14 sqrt8_260 12 1 314 3 728 1 198 10.48 1 101 130 11.17 70.47 89.15
15 radd_250 13 1 405 4 332 1 482 13.00 1 267 219 14.17 70.75 85.22
16 adr4_197 13 1 498 4 684 1 644 15.13 1 332 226 11.60 71.56 86.25
17 misex1_241 15 2 100 7 556 2 744 20.75 1815 312 24.73 75.98 88.63
18 rd73_252 10 2 319 6 876 2 370 7.29 1811 296 8.83 73.66 87.51
19 cycle10_2_110 12 2 648 9 700 2 928 10.55 2 302 395 14.37 76.27 86.51
20 square_root_7 15 3 089 9 335 2 752 16.94 2 753 370 20.10 70.51 86.56
21 sqn_258 10 4 459 13 829 4 918 9.01 3 369 398 9.45 75.64 91.91
22 inc_237 16 4 636 14 579 5 486 37.82 3 846 608 37.80 73.62 88.92
23 rd84_253 12 5 960 22 785 7 336 14.58 4 970 717 15.02 78.19 90.23
24 root_255 13 7 493 29 689 10 244 16.76 5 919 694 17.26 80.06 93.23
25 co14_215 15 7 840 28 291 8 552 26.39 6 640 857 24.63 76.53 89.98
26 mlp4_245 16 8 232 28 963 9 264 24.00 7 013 1 020 28.83 75.79 88.99
27 sym9_148 10 9 408 27 995 10 036 9.70 6 765 904 11.99 75.83 90.99
28 life_238 11 9 800 33 688 11 192 12.24 7 916 1 073 12.22 76.50 90.41
29 max46_240 10 11 844 34 640 10 676 10.99 9 580 1 470 12.07 72.34 86.23
30 clip_206 14 14 772 61 854 21 818 21.67 12 198 1 538 23.95 80.28 92.95
31 9symml_195 11 15 232 54 676 18 304 12.92 12 570 1 708 16.44 77.01 90.67
32 sym9_193 11 15 232 51 570 15 972 13.69 12 959 1979 16.54 74.87 87.61
33 dist_223 13 16 624 60 240 19 478 20.19 14 073 1986 19.97 76.64 89.80
34 sym10_262 12 28 084 93 147 28 756 19.07 24 017 3 630 23.13 74.22 87.38
35 urf3_279 10 60 380 195 298 66 474 26.23 50 700 8 662 33.17 74.04 86.97
36 plus63mod4096_163 13 56 329 222 417 72 346 30.97 48 818 6 875 40.40 78.05 90.50
37 urf6_160 15 75 180 325 841 119 700 48.70 72 316 13 962 56.80 77.81 88.34
38 hwb9_119 10 90 955 306 500 103 090 37.51 72 358 9 637 43.95 76.39 90.65
39 ground_state_estimation_10 13 154 209 420 548 130 214 82.88 44 609 23 977 80.05 89.39 81.59
40 urf4_187 11 224 028 715 546 240 168 87.22 174 385 24 469 111.86 75.63 89.81

DQM 方法在 SWAP 门和 ST 门上取得的优势主要源于以下几点原因: (1) DQM 在映射逻辑量子比特时同时
考虑了量子线路结构、分布式系统的网络拓扑以及 QPU 内量子比特的排列方式, 而 DQP 仅考虑了量子线路本身