Page 497 - 《软件学报》2025年第5期

朱鹏程 等: 面向分布式超导量子计算架构的量子线路映射 2397

不同以外, 该线性网络包含的 QPU 类型及数量均和图 1 所示的二维网络相同; 为使得网络中的每个 QPU 均参与
量子线路映射, 我们还构建了由 1 000 个随机线路组成的测试集, 测试集中的每个线路均包含 24 个量子比特. 根
据 CNOT 门数的不同可将该随机线路测试集划分为 10 个子集, 其中每个子集均包含 100 个仅由 CNOT 门组成的
随机线路, 各子集对应的 CNOT 门数分别为{100, 200, 300, 400, 500, 600, 700, 800, 900, 1 000}. 本文 DQM 算法在
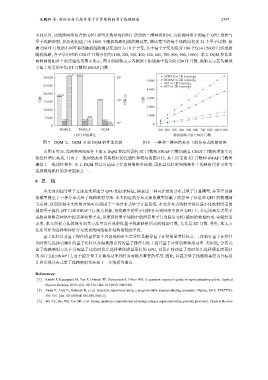
两种网络拓扑上的实验结果图 8 所示, 图 8 的横轴表示各测试子集线路中包含的 CNOT 门数, 纵轴表示在各测试
子集上所需的平均 ST 门数和 SWAP 门数.

1 151.59 30 823.48
30 000 10 3 #SWAP of 1D topology
5 000 #SWAP of 2D topology
#ST of 1D topology
25 000 #ST of 2D topology
4 000
20 000
18 369.03
门数 15 000 15 489.5 10 2 时间 (s) 门数 3 000
2 000
10 000
1 000
5 000 16.69
3 028.78 2 958.73 2 802.43
9.28 10 1
0 0
DQM_L DQM_S DQM 100 200 300 400 500 600 700 800 900 1 000
3 种比对的算法 测试线路中的 CNOT 门数
图 7 DQM_L、DQM_S 和 DQM 的性能比较 图 8 一维和二维网络拓扑上的分布式映射结果
由图 8 可知, 在两种网络拓扑上本文 DQM 算法所需的 ST 门数和 SWAP 门数均随着 CNOT 门数的增加呈近
似线性增长关系, 且由于二维网络拓扑具备较好的连通性和较短的图直径, 其上所需的 ST 门数和 SWAP 门数普
遍低于一维线性拓扑. 本文 DQM 算法可适应于任意网络拓扑结构, 因此其在特定网络拓扑上的映射代价可作为
选择网络拓扑的参考因素之一.

6 总 结

本文面向超导量子互连技术和超导 QPU 的技术特征, 抽象出一种可扩展的分布式量子计算模型, 并基于该抽
象模型提出了一种分布式量子线路映射方法. 本文构造的分布式抽象模型屏蔽了底层量子信道和 QPU 的物理细
节差异, 从而使得本文映射方法可以适用于一类分布式量子计算系统. 本文分布式映射方法以最小化映射所需的
辅助量子操作 (ST 门和 SWAP 门) 数为目标, 将线路中的量子比特分布到网络中的各 QPU 上, 并运用启发式量子
态路由策略在网络中按需移动量子态, 从而使得量子线路中的所有量子门均满足 QPU 施加的物理约束. 实验结果
表明, 本文所提方法较现有同类方法可以有效降低量子线路映射所需的辅助门数, 尤其是 ST 门数. 另外, 本文方
法还可作为选择和评价分布式系统网络拓扑结构的辅助手段.
量子比特以及量子操作质量存在不容忽视的时空差异性是超导量子计算的显著特征之一, 在执行量子计算任
务时优先选择更健壮的量子比特以及保真度更高的量子操作有助于提升量子计算的整体成功率. 类似的, 分布式
量子线路映射方法在分配量子比特时优先选择整体质量更好的 QPU, 以及在移动量子态时优先选择保真度更好
的 ST 门或 SWAP 门, 对于提升量子计算成功率同样有着极其重要的作用. 因此, 以提升量子线路保真度为目标设
计和实现分布式量子线路映射方法是下一步的研究重点.

References:
[1] Krantz P, Kjaergaard M, Yan F, Orlando TP, Gustavsson S, Oliver WD. A quantum engineer’s guide to superconducting qubits. Applied
Physics Reviews, 2019, 6(2): 021318. [doi: 10.1063/1.5089550]
[2] Arute F, Arya K, Babbush R, et al. Quantum supremacy using a programmable superconducting processor. Nature, 2019, 574(7779):
505–510. [doi: 10.1038/s41586-019-1666-5]
[3] Wu YL, Bao WS, Cao SR, et al. Strong quantum computational advantage using a superconducting quantum processor. Physical Review