Page 84 - 《软件学报》2024年第4期

1662 软件学报 2024 年第 35 卷第 4 期

2%以内, 表明本文所提的方法对于邻居数量(N)不敏感.
• 主动样本的比例(β)
为了展示主动样本的比例(β)对 LCAL 算法的影响, 本文在不同的主动样本选择比例β下对 LCAL, Entropy
和 K-means 方法进行了比较. 如图 6(b)所示, 横坐标指主动样本比例. 随着主动样本比例的增加, 通过匹配纠
正, 可以纠正更多相似的公共类和开放类样本, 所有主动学习的策略都带来了模型效果的显著提高. 值得注
意的是: 在不同的样本选择比例下, LCAL 算法始终远远高于现有的主动学习方法, 进一步表明本文所提的方
法可以挑选到更全面、更有价值的阈值模糊的样本, 通过主动标注, 可以有效地促进了开放类样本和公共类
样本的分离, 显著地提高了模型的效果.

(a) 邻居数量消融实验 (b) 主动样本比例消融实验
图 6 邻居数量与主动样本比例对 LCAL 算法的影响
• 公共类和开放类的特征分布
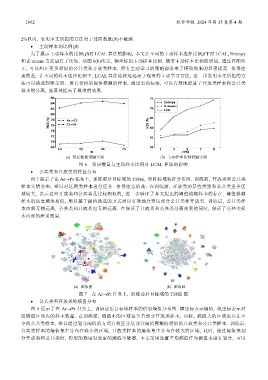
图 7 展示了在 Ar→Pr 任务上, 训练前后目标域的 TSNE, 即目标域特征分布图. 训练前, 开放类和公共类
样本交错分布, 难以对这两类样本进行区分. 值得注意的是: 在训练前, 开放类的某些类别和公共类重合区
域较大, 表示这些开放类和公共类是比较相似的, 进一步验证了本文提出的阈值模糊样本的存在. 阈值模糊
样本的信息熵值相似, 所以基于阈值挑选的方式难以有效地分开这部分公共类和开放类. 训练后, 公共类样
本内部互相远离, 公共类和开放类也互相远离. 在保证了开放类和公共类分离效果的同时, 保证了公共类样
本内部的辨别效果.

(a) 训练前 (b) 训练后
图 7 在 Ar→Pr 任务上, 训练前后目标域的 TSNE 图
• 公共类和开放类的熵值分布
图 8 展示了在 Ar→Pr 任务上, 训练前后目标域样本的信息熵值分布图. 横坐标表示熵值, 纵坐标表示对
应熵值区间内的样本数量. 在训练前, 熵值小的区域包含着部分开放类样本; 同样, 熵值大的区域也存在不
少的公共类样本, 难以通过划分阈值的方式有效区分这部分阈值模糊的相似的开放类和公共类样本. 训练后,
公共类样本的熵值集中分布在较小的区域, 开放类样本的熵值集中分布在较大的区域, 此时, 通过阈值来划
分开放类和公共类时, 模型的效果对设定的阈值不敏感. 本文采用设置平均熵值作为阈值来进行划分, 可以