Page 268 - 《软件学报》2021年第5期

1492 Journal of Software 软件学报 Vol.32, No.5, May 2021

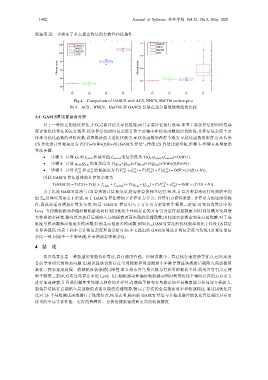
敛速度,进一步验证了本文提出算法的有效性和优越性.

1.5
120 GASCS GASCS
NNCS NNCS
HeCOS HeCOS
100 ACS
ACS
1.0
Fitness value 60 Fitness value 0.5
80
40
0.0
20
F5 F5 F5 F5 F7 F7 F7 F7
Fig.4 Comparison of GASCS with ACS, NNCS, HeCOS on box-plot
图 4 ACS、NNCS、HeCOS 和 GASCS 算法在部分函数的箱线图比较

3.4 GASCS算法复杂度分析
对于一种给定的优化算法,不仅需要评估其寻优性能,而且需要评估运行效率.本节主要从算法的时间复杂
度评估优化算法的运行效率.优化算法的时间复杂度计算主要集中在优化函数的评价阶段,其算法复杂度主要
体现为优化函数的评价次数.设置算法最大进化代数为 W,优化函数的种群个数为 N,优化函数的维度为 D.传统
CS 算法的计算复杂度为 T(CS)=O(W×(f(D)+N)).GASCS 算法与传统 CS 算法比较可知,步骤 3~步骤 6 是增加的
算法步骤.
• 步骤 3. 计算 G r 和 f r,best 和最差值 f r,worst 的复杂度为 T(G r +f r,best +f r,worst )=O(W×1).
• 步骤 4. 计算 q r,m ,Q r,m 的复杂度为 T(q r,m +Q r,m )=T(q r,m )+T(Q r,m )=O(W×(f(D)+N)).
• 步骤 5. 计算 F ()j , rm 和 a ()j , rm 的复杂度为 (TF ()j , r m + a ()j , rm ) T= (F ()j , rm ) T+ (a ()j , r m ) = O(W × ( ( )f D + N )) .
因此,GASCS 算法总体的计算复杂度为
TGASCS ) TCS= ( ) T+ (G + f + f ) T+ (q + Q ) T+ (F ()j + a ( )j ) = O(W × ( ( )f D + N )) .
(
r , r best , r worst , rm , rm , r m , rm
为了比较 GASCS 算法与 CS 算法的计算复杂度,将每种算法独立运行 30 次,计算各种算法运行时间的平均
值 T m ,具体结果如表 1 所述.由于 GASCS 算法增加了计算引力合力、计算引力惯性质量、计算引力加速度等操
作,因此会适当增加计算复杂度.但是 GASCS 算法引入了万有引力定律和牛顿第二定律,对布谷鸟算法中的
Levy 飞行随机游动和偏好随机游动同时利用优化个体间存在的万有引力进行加速搜索,同时利用概率变异增
大种群的多样性,避免算法执行后期陷入局部极值点而出现的迟滞现象,因此能更快搜索到全局最优解.对于高
维度单模函数和高维度多模函数,特别是高维度多模函数,例如 F 16 ,GASCS 算法的优化效率相比于传统 CS 算法
有显著提高.由表 1 和本节计算复杂度理论分析可知:本文提出的 GASCS 算法计算复杂度与传统 CS 算法的复
杂度一致,同属于一个数量级,并未增加算法复杂度.

4 结 论
布谷鸟算法是一种新型的智能优化算法,具有通用性强、控制参数少、算法执行速度快等优点,已经成为
目前学者研究的热点问题.但是该算法仍然存在全局搜索和局部搜索不平衡导致算法搜索后期陷入局部极值
最优、搜索速度较慢、收敛精度较低的局限性.本文将布谷鸟巢穴视为有质量的物质个体,利用万有引力定律
和牛顿第二定律,对布谷鸟算法中的 Levy 飞行随机游动和偏好随机游动同时利用优化个体间存在的万有引力
进行加速搜索,并且采用概率变异增大种群的多样性,有效地平衡布谷鸟算法的全局搜索能力和局部开采能力,
避免算法执行后期陷入局部极值点而出现的迟滞现象,提高了算法的全局搜索效率和收敛精度.通过用优化算
法对 26 个基准测试函数进行了性能仿真,结果表明,提出的 GASCS 算法与其他改进智能优化算法相比具有更
优秀的全局寻优性能、更好的鲁棒性、更快的搜索速度和更高的收敛精度.