Page 267 - 《软件学报》2021年第5期

傅文渊:具有万有引力加速机理的布谷鸟搜索算法 1491

敛后期会出现迟滞和陷入局部最优值的现象.与之对比,GASCS 算法只需要较少的迭代次数就能搜索到全局最
优解.对于 F9,由于 GASCS 算法能搜索到理论最优值 0,而数学上无法对 0 取对数,因此用数学软件作图时无法
[2]
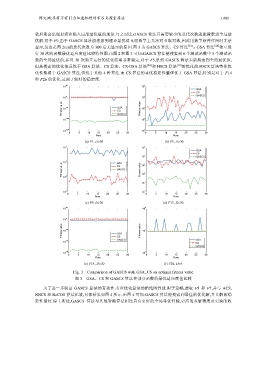
显示,这也是图 2(c)的迭代次数为 300 后无显示的原因.图 3 为 GASCS 算法、CS 算法 与 GSA 算法 [24] 独立运
行 30 次的函数最优适应度值比较特性图.由图 2 和图 3 可知:GASCS 算法能搜索到 6 个测试函数中 5 个测试函
数的全局最优值,并且 30 次独立运行的优化结果非常稳定.对于 F5,虽然 GASCS 算法未能搜索到全局最优值,
但是搜索的优化值远优于 GSA 算法、CS 算法、CS-GSA 算法 [22] 和 HSCS 算法 [18] 的优化值.HSCS 算法整体优
化性能弱于 GASCS 算法,但优于其他 4 种算法.而 CS 算法的寻优稳定性整体优于 GSA 算法,特别是对于 F14
和 F26 的优化,达到了较好的稳定度.
50 5
10 10
GSA
CS
10 0 10 4 GASCS
Fitness value 10 -50 GSA Fitness value 10 3
CS
GASCS
10 -100 10 2

-150 1
10 10
0 5 10 15 20 25 30 0 5 10 15 20 25 30
Runs Runs
(a) F1, D=30 (b) F5, D=30
2
10 10 3
GSA
CS
2
10 GASCS
1
10 GSA 10 1
Fitness value GASCS Fitness value 10 0
CS
0
10
-1
10
10 -1 10 -2
0 5 10 15 20 25 30 0 5 10 15 20 25 30
Runs Runs
(c) F9, D=30 (d) F13, D=30
10 20 -10 0
0
10
Fitness value 10 -20 GSA Fitness value -10 1

CS
GASCS GSA
-40
10 CS
GASCS
10 -60 -10 2
0 5 10 15 20 25 30 0 5 10 15 20 25 30
Runs Runs
(e) F14, D=30 (f) F26, D=4
Fig. 3 Comparison of GASCS with GSA, CS on optimal fitness value
图 3 GSA、CS 和 GASCS 算法在部分函数的最优适应度值比较

为了进一步验证 GASCS 算法的有效性,考查优化算法的箱线图性能.限于篇幅,选取 F5 和 F7,并与 ACS,
NNCS 和 HeCOS 算法比较,具体结果如图 4 所示.由图 4 可知:GASCS 算法能搜索到最佳的优化解,并且解的稳
定性最好.综上所述,GASCS 算法与其他智能算法相比具有更好的全局寻优性能,更高的求解精度及更快的收