Page 7 - 摩擦学学报2025年第5期

第 5 期 蔡胜民, 等: 多叶型空气箔片轴承静动特性试验研究 641

200 Pull 3 动态特性试验
150 Push
3.1 动态特性试验细节
100
50 动态特性试验的目的主要是获取多叶型空气箔
Force/N −50 0 片轴承的刚度和阻尼，为此搭建了动态特性试验台，
如图7所示. 试验台的组成部分和静态试验台类似，将
−100 直线步进电机换成电磁激振器，并在静态力传感器末
−150
端加上动态力传感器. 电磁激振器可以产生预期的激
−200
−200 −100 0 100 200 振力，静态力传感器可以对初始预紧力进行测量，动
Displacement/μm
态力传感器可以对激振力进行实时监测.
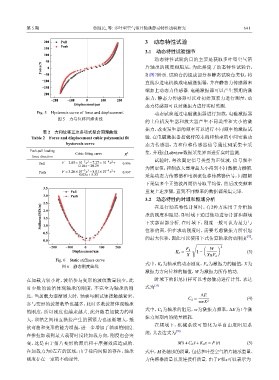
Fig. 5 Hysteresis curve of force and displacement 动态试验通过电磁激振器进行加载，电磁激振器
图 5 力与位移回滞曲线
的上位机发生器和放大器产生不同类型和大小的激
振力，改变发生器的频率可以进行不同频率的激振试

表 2 力和位移三次多项式拟合回滞曲线
Table 2 Force and displacement cubic polynomial fit 验. 在电磁激振器加载杆的末端和轴承的中间安装动
hysteresis curve 态力传感器，力和位移传感器信号通过NI采集卡采
Push-pull loading
Cubic fitting curve R 2 集，并通过Labview数据采集界面进行实时监测.
force direction
试验时，每次固定信号类型为正弦波，信号频率
−5 3
−4 2
Pull F = 2.85×10 x −7.27×10 x + 0.996
0.16x−20.29
为固定值，控制放大器增益大小得到不同激振力振幅.
−5 3
−4 2
Push F = 3.26×10 x −8.01×10 x + 0.997
0.03x+5.33 采集动态力传感器和电涡流位移传感器信号，同振幅
下采集多个正弦波周期信号取平均值，然后改变频率
3.5

Pull 重复上述步骤，直到不同频率的数据都采集完毕.
3.0 Push
3.2 动态特性的时域和频域分析
Stiffness/(MN/m) 2.5 承的刚度和阻尼，即时域下通过做功进行计算和频域
在进行动态特性计算时，有2种方法用于分析轴
2.0
1.5
下实部虚部分析. 在时域下，刚度一般可认为是力与
1.0
0.5 位移的商，但在求动刚度时，需要考虑激振力所引起
的最大位移，因此可以使用下式估算轴承的动刚度 ：
[27]
0.0
−200 −100 0 100 200 Å W ã 2
Displacement/μm K d = F d 1− (3)
X XπF d
Fig. 6 Static stiffness curve
式中， K d 为轴承的动态刚度， F d 为激振力的幅值， X为
图 6 静态刚度曲线
激振力方向位移的幅值， W为激振力所作的功.
在加载力较小时，波箔参与变形的波纹数量较少，此 时域下的阻尼同样可以考虑做功进行计算，表达
时少数的波箔体现轴承的刚度，不完全为轴承的刚 式为 [15]
度，当加载力逐渐增大时，轴承与测试轴接触越紧密， ∆E
C d = 2 (4)
参与变形的波箔数量也越多，此时多数波箔体现轴承 πwX
式中， C d 为轴承的阻尼， w为激振力频率， ∆E为1个激
的刚度，所以刚度也越来越大. 此外随着加载力的增
大，顶箔之间相互搭接产生的预紧力也逐渐增大，抵 振力周期内的能量损耗.
在频域下，机械系统可简化为单自由度阻尼系
抗弯曲和变形的能力增强，进一步增加了轴承的刚度.
统，其表达式为 [28]
在推拉加载到最大载荷时反转加载方向，刚度也会突
变，这是由于箔片变形的滞后和干摩擦效应造成的. M ¨x+C d ¨x+ K d x = F (t) (5)
在加载力为0左右的区域，由于径向间隙的存在，轴承 式中， M是轴承的质量，包括多叶型空气箔片轴承重量、
刚度存在一定的不确定性. 力传感器质量以及连接杆质量. 由于F和x可以表示为