Page 58 - 摩擦学学报2025年第5期

692 摩擦学学报（中英文） 第 45 卷

Slippery
wall (W3)
Periodic Pressure Outlet
boundary Γ1 outlet W1
W2
Rotating Rotor Stator
wall (W4) Periodic W4 W3
boundary Γ2
Pressure
inlet
Other static walls Inlet
(W1 and W2)
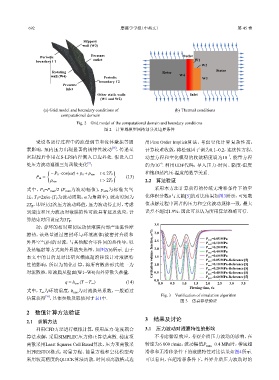
(a) Grid model and boundary conditions of (b) Thermal conditions
computational domain
Fig. 2 Grid model of the computational domain and boundary conditions
图 2 计算域模型网格划分及边界条件

受设备运行过程中的流量调节和流体激振等因 用First Order Implicit算法，考虑空化计算复杂性高，
[38]
素影响，泵内压力出现显著的规律性波动 ，传递至 计算较难收敛，将松弛因子调为0.1~0.2，连续性方程、
−3
密封腔后作用在S-LFS内径侧入口边界处. 假设入口 动量方程和空化模型的收敛精度设为10 ，能量方程
[5]
−6
处压力波动遵循三角函数变化 ： 的为10 . 利用UDF代码，导入压力-时间、黏度-温度
® ´
和饱和蒸汽压-温度的数学关系.
− P 0 ·cos(ωt)+ p 0 + p atm t ⩽ 2T P
P in = (13)
p atm t > 2T P 2.2 算法验证
式中，P =P max /2 (P max 为波动幅值)，p atm 为标准大气 采用本方法计算获得的传统无滑移条件下的空
0
压；T =2π/ω (T 为波动周期；ω为角频率). 波动时间为 化体积分数α与文献[5]的对比结果如图3所示，可知数
P
P
2T ，即经历2次压力波动峰值，压力波动停止时，考虑 值求解过程中两者的压力和空化波动规律一致，最大
P
到速度和压力波动对液膜特性可能具有延迟效应，计 误差不超过1.9%，因此可以认为所用算法准确可行.
算结束时间设定为3T .
P

动、静环的相对剪切运动使液膜内部产生黏性摩 3.5
擦热，该热量通过密封环与环境流体(被密封介质和 3.0 P max =0.05 MPa
外界空气)间的对流，与其他配合零件间的热传导，以 2.5 P max =0.10 MPa
及热辐射等方式向外界散失热量，如图2(b)所示. 由于 2.0 P max =0.20 MPa
P max =0.40 MPa
本文中的目的是对比研究槽底超滑移设计对液膜特 Cavitation volume fraction, α/% 1.5 P max =0.60 MPa
P max =0.05 MPa-Reference [5]
性的影响，所以为简化计算，将所有散热形式统一为 1.0 P max =0.10 MPa-Reference [5]
P max =0.20 MPa-Reference [5]
对流散热，即液膜从壁面(W1~W4)向外界散失热量. 0.5 P max =0.40 MPa-Reference [5]
P max =0.60 MPa-Reference [5]
q = h con (T −T ∞ ) (14) 0.0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Flowing time, t/s
式中，T 为环境温度，h con 为对流换热系数，一般通过
∞
Fig. 3 Verification of simulation algorithm
[39]
估算获得 ，具体参数及取值列于表1中.
图 3 仿真算法验证

2 数值计算方法验证

3 结果及讨论
2.1 求解方法
利用CFD方法进行模拟计算，使用压力-速度耦合 3.1 压力波动对液膜特性的影响
算法求解，采用SIMPLEC压力修正算法离散. 梯度项 不考虑黏温效应，考察介质压力波动的影响，在
离散采用Least Squares Cell Based算法，压力项离散采 转速为6 000 r/min，波动幅值P max =0.4 MPa时，槽底超
用PRESTO!格式，动量方程、能量方程和空化模型均 滑移和无滑移条件下的液膜特性对比结果如图4所示.
采用较高精度的QUICK算法离散，时间项离散格式选 可以看出，在超滑移条件下，外界介质压力波动时的