Page 56 - 《摩擦学学报》2021年第1期

第 1 期 沈锦龙, 等: 考虑界面粗糙度动态变化的点接触弹流润滑特性研究 53

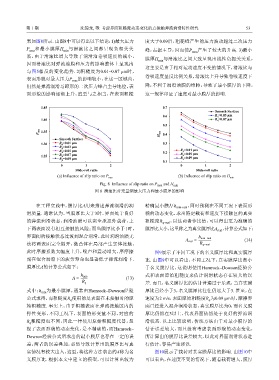
果如图8所示. 由图8中可以得出以下结论：1)最大压力 度大于0.09后，粗糙峰产生的压力波动超过二次压力
P max 和最小膜厚H min 与滑滚比之间都呈现负相关关 峰，占据主导，因而使P max 产生了较大的升高. 3)最小
系，由于滑滚比增大导致了润滑油卷吸速度的减小，
膜厚H min 与滑滚比之间大致呈现出线性负相关关系，
因而滑滚比对弹流油膜和压力的影响整体上呈现出
这主要是由于相对运动速度不变的情况下，滑滚比与
与图5相反的变化趋势. 2)粗糙度为0.01~0.07 μm时，
卷吸速度呈反比例关系，滑滚比上升导致卷吸速度下
表面形貌对最大压力P max 的影响较小，在这一区域内，
仍然是弹流润滑马蹄形的二次压力峰占主导地位，表 降，不利于润滑油膜的维持，导致了最小膜厚的下降，
面形貌的影响逐渐上升，直至与之相当，在表面粗糙 这一规律印证了速度对最小膜厚的影响.

1.45 0.7
Smooth Surface
R q =0.03 μm
0.6
1.40 R q =0.07 μm
0.5
P max 1.35 H min 0.4
Smooth Surface
1.30 R q =0.01 μm 0.3
R q =0.03 μm
R q =0.05 μm 0.2 R q =0.01 μm
R q =0.07 μm R q =0.05 μm
1.25
R q =0.09 μm R q =0.09 μm
0.1
0 1 2 0 1 2
Slide-roll ratio Slide-roll ratio
(a) Influence of slip ratio on P max (b) Influence of slip ratio on H min
Fig. 8 Influence of slip ratio on P max and H min
图 8 滑滚比对无量纲最大压力和最小膜厚的影响

在工程实践中，膜厚比Λ用来描述弹流润滑的润 精确最小膜厚h min-real ，同时预测在不同工况下表面形
滑质量. 通常认为，当膜厚比大于3时，界面处于良好 貌的动态变化，求出特定载荷和速度下接触区的真实
的弹流润滑状态，润滑油膜可以完全承担外载荷，上 粗糙度R q-real ，以这两者作比值，可以得出更为准确的
下两表面没有相互接触的风险；而当膜厚比小于1时， 膜厚比大小，这里称之为真实膜厚比Λ ，计算公式如下：
real
界面间的接触状态过渡到混合润滑，此时润滑油膜无 h min−real
Λ real = (14)
法将两表面完全隔开，微凸体在局部产生实体接触， R q−real
此时摩擦系数大幅度上升，噪声和震动增大，摩摩擦 图9展示了不同工况下的名义膜厚比和真实膜厚
副在混合润滑下的疲劳寿命也显著低于弹流润滑下. 比. 由图9中可以看出，不同工况下，真实膜厚比都小
膜厚比Λ的计算公式如下： 于名义膜厚比，这说明使用Hamrock–Dowson经验公
式和表面原始粗糙度来估计润滑状态存在较大的误
h min
Λ = (13)
R q 差. 而且，名义膜厚比的估计普遍过于乐观，当真实膜
式中：h min 为最小膜厚，通常由Hamrock–Dowson经验 厚比已经小于3，名义膜厚比往往仍远大于3. 甚至，在
公式求得，而粗糙度R 使用的是表面在未接触时的原 速度为2 m/s，表面原始粗糙度R 为0.09 μm时，摩擦界
q q
始粗糙度. 事实上，由于粗糙表面在弹流接触区内的 面已经进入混合润滑状态，真实膜厚比为0，而名义膜
弹性变形，不同工况下，表面的形变量不同，对应的 厚比仍然在3以上，代表界面依然处于良好的弹流润
R 粗糙度也不同，因此一律使用原始粗糙度代替，忽 滑状态. 以上比较说明，传统方法由于对最小膜厚的
q
视了表面形貌的动态变化，是不精确的，而Hamrock– 估计误差较大，而且没有考虑表面形貌的动态变化，
Dowson经验公式所求出的最小膜厚也存在一定的误 所计算出的膜厚比误差较大，以此对界面润滑状态进
差，两者的误差叠加，必然导致计算出的膜厚比与真 行估计，容易产生谬误.
实情况有较大出入，这里，将这种方法求出的Λ称为名 图10展示了载荷对真实膜厚比的影响. 由图10中
义膜厚比. 根据本文中建立的模型，可以计算出较为 可以看出，在速度不变的情况下，随着载荷增大，膜厚