Page 27 - 《摩擦学学报》2020年第6期

710 摩 擦 学 学 报 第 40 卷

(a) P h2 P h1 P h3

1

σ h1 σ h2
B A C

I II
z

(b) (c)

D D
′ ′
P v1 σ I-1 σ II-1 P v2
1
y y
σ II-I
σ I-II
P v1
P v2
A A
I II I II

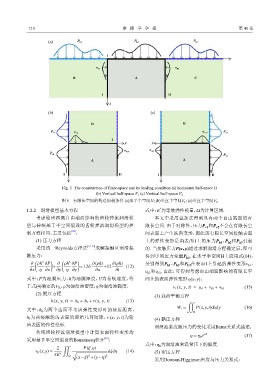
Fig. 5 The construction of finite-space and its loading condition (a) horizontal half-space H
(b) Vertical half-space V 1 (c) Vertical half-space V 2
图 5 有限长空间的构造加载条件 (a)水平半空间H；(b)垂直半空间V 1 ；(c)垂直半空间V 2
*
1.2.2 润滑模型基本方程 式中：E 为等效弹性模量，Ω为计算区域.
考虑轮齿两侧自由端面影响的齿轮弹流润滑模 本文中采用叠加法得到具有两个自由端面的有
型与传统基于半空间假设的齿轮弹流润滑模型的控 限长空间. 由于对称性，压力P 和P 不会在有限长空
v2
v1
[20]
制方程相同，主要包括 ： 间表面上产生法向变形，因此该有限长空间接触表面
(1) 压力方程 上的弹性变形是由表面1上的压力P 、P 和P 引起
h1
h3
h2
采用统一Reynolds方程法 [21-22] 求解接触区润滑接 的. 当接触压力P(x，y)通过求解润滑方程确定后，即可
触压力： 得到中间压力变量P . 在水平半空间H上应用式(14)，
h1
( ) ( )
3
3
∂ ρh ∂P ∂ ρh ∂P ∂(ρh) ∂(ρh) 分别得到P 、P 和P 在表面1上引起的弹性变形v 、
+ =12U +12 (12) h1 h2 h3 h1
∂x η ∂x ∂y η ∂y ∂x ∂t v 和v . 由此，可得到考虑自由端面影响的有限长空
h3
h2
式中：P为油膜压力，h为油膜厚度，U为卷吸速度，等 间上的表面弹性变形v (x，y)：
f
于式(4)确定的V ，ρ为润滑油密度，η为润滑油黏度. v f (x, y, t) = v h1 + v h2 + v h3 (15)
K
(2) 膜厚方程
(3) 载荷平衡方程
h(x, y, t) = h 0 + h 1 +v(x, y, t) (13) "
W t = P(x,y,t)dxdy (16)
式中：h 为两个齿面不考虑弹性变形时的接近距离， Ω
0
h 为两接触轮齿表面的原始几何间隙，v (x，y，t)为轮 (4) 黏压方程
1
齿表面的弹性变形. 润滑油黏度随压力的变化采用Barus关系式描述：
传统齿轮弹流润滑模型中计算表面弹性变形均
η = η 0 e αP (17)
[23]
采用基于半空间假设的Boussinesq积分 ：
式中：η 为润滑油常温常压下的黏度.
0
2 " P(ξ,η)
v h (x,y) = √ dξdη (14) (5) 密压方程
πE ∗ Ω 2 2
(x−ξ) +(y−η)
采用Dowson-Higginson密度与压力关系式：