Page 68 - 《爆炸与冲击》2026年第01期

第 46 卷 王天召，等： 水下接触爆炸气泡脉动特性的理论研究 第 1 期

2
3 ˙ 2 3
πρ 0 R R + πR p ∞ + E(R h ) = Y h (1)
h
h
h
3
R h 为接触爆炸脉动气泡半
式中： ρ 0 为无穷远处流体的密度；下标“ h ”表示接触爆炸条件下的物理量；
2
V h = πR 3 h R h 为接
˙
径，即起爆点到气泡表面上任意一点的距离，显然，若气泡为半球形气泡，则气泡体积 ；
3
E (R h ) 为气泡内
触爆炸气泡脉动速度； p ∞ 为与气泡脉动中心初始位置同一深度的无穷远处流场的压力；
R h,0 ，
能； Y h 为接触爆炸气泡的总能量。在气泡脉动初始时刻，气泡脉动速度为零，气泡脉动初始半径为
2
Y h = E h,0 + πp ∞ R 3 h,0 ，代入式 (1) 得：
则：
3
2 2
3 ˙ 2 3 3
h h h h,0
πρ 0 R R + πR p ∞ + E(R h ) = E h,0 + πR p ∞ (2)
3 3
w t
式中：E h, 0 为接触爆炸时气泡的初始内能，内能的变化满足 E h,0 − E (R h ) = 0 p h dV h ，则有：
2 w t
3 ˙ 2 3 3
πρ 0 R R + π(R −R )p ∞ − p h dV h = 0 (3)
h
h
h,0
h
3 0
p h 的计算公式为：
气泡内爆轰产物的压力变化遵循幂指数等熵膨胀规律，
Å ã λ
V h,0
p h = p c + p h,0 (4)
V h
Å ã λ
W
p h,0 = K ，V 0 为接触爆炸时气泡
式中： p c 为水的饱和蒸汽压； p h,0 为半球形气泡内部初始压力，且 h,
V h,0
W 为 5 。将式 (3) 两边同时对时间 t 求导
的初始体积， TNT 当量， λ 为爆轰产物的绝热指数， K 取 1.39×10
并且进行化简，可以得到接触爆炸条件下气泡脉动动力学方程：
3 1
¨
˙
2
R h +R h R h = (p h − p ∞ ) (5)
2 ρ 0
R m (ρ 0 /∆p) 1/2 分别作为长度、压力以及时间的特征量，得到无量纲的接
在此基础上，以 R m 、 ∆p 以及
触爆炸气泡脉动方程：
3
˙
¨
∗2
R +R R = p −1 (6)
∗
∗
∗
2 h h h h

式中：上标“*”表示参数为无量纲气泡脉动参 Contact explosion
数 。 R m 为 自 由 场 气 泡 最 大 半 径 ， ∆p = p ∞ − p v ， 0.12 Free-field

p v 为饱和蒸汽压，可以忽略不计。
其中
0.09
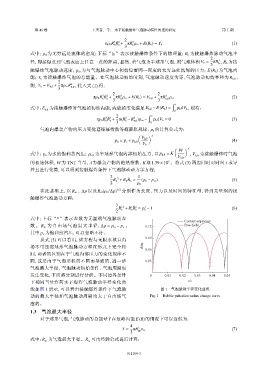
从式 (5) 可以看出，该方程与无限水域自由
场不可压缩球形气泡脉动方程在形式上完全相 R/m 0.06
同，两者的区别在于气泡内部压力的变化规律不
同，这是由于气泡形状的不同而导致的，进一步 0.03
气泡最大半径、气泡脉动初始条件、气泡周期也
发生变化，下面将分别进行分析。不同边界条件 0 0.01 0.02 0.03 0.04 0.05
下相同当量炸药水下爆炸气泡脉动半径变化曲 t/s
线如图 1 所示，可以看出接触爆炸条件下气泡脉 图 1 气泡脉动半径变化曲线
动的最大半径和气泡脉动周期均大于自由场气 Fig. 1 Bubble pulsation radius change curve
泡的。
1.3 气泡最大半径
E (R) 的情况下可以近似为：
对于球形气泡，气泡脉动的总能量 Y 在忽略内能
4
3
Y = πR p ∞ (7)
m
3
式中：R 为气泡最大半径。R 可由经验公式进行计算：
m
m
011104-3