Page 51 - 《爆炸与冲击》2025年第6期

第 45 卷 刘红岩，等： 考虑裂隙粗糙度的岩体单轴压缩动态损伤模型 第 6 期

30 29 10.0

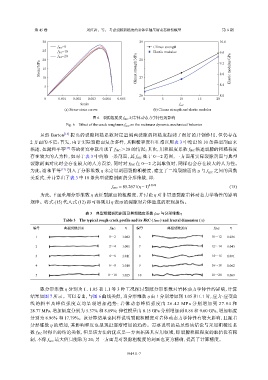
f JRC =0 Climax strength
25 f JRC =10 Elastic modulus 9.6
f JRC =20
20 28 9.2
Stress/MPa 15 Climax strength/MPa Elastic modulus/GPa

10 27 8.8
5 8.4

26 8.0
0 0.001 0.002 0.003 0.004 0.005 0 5 10 15 20
Strain f JRC
(a) Stress-strain curves (b) Climax strength and elastic modulus
图 6 裂隙粗糙度 f JR 对岩体动态力学特性的影响
C
Fig. 6 Effect of the crack roughness f JRC on the rockmass dynamic mechanical behavior

虽然 Barton [16] 提出的裂隙粗糙系数对定量刻画裂隙的粗糙度起到了很好的开创作用，但仍存在
2 方面的不足：首先，由于实际裂隙面复杂多样，其粗糙程度往往难以用表 3 中给出的 10 条典型剖面来
描述，如谢和平等 [17] 等的研究中就出现了 f JRC ＞20 的情况；其次，用粗糙度系数 f JRC 描述裂隙的粗糙程度
存在较大的人为性，如对于表 3 中的第一条剖面，其 f JRC 处于 0～2 范围，一方面用实际裂隙剖面与典型
f JRC 在 之间取值时，同样也会存在较大的人为性。
裂隙剖面对比时会存在较大的人为误差，同时对 0～2
为此，谢和平等 [17] 引入了分形维数 η 来定量刻画裂隙粗糙度，建立了二维裂隙面的 η 与 f C 之间的函数
JR
关系式，并计算出了表 3 中 10 条典型裂隙剖面的分形维数，即：
f JRC = 85.2671(η−1) 0.5679 (15)
为此，下面采用分形维数 η 表征裂隙面的粗糙度，并讨论 η 对非贯通裂隙岩体动态力学特性的影响
规律。将式 (15) 代入式 (12) 即可得到用 η 表示的裂隙对岩体造成的宏观损伤。

η
表 3 典型粗糙裂隙剖面及其粗糙度系数 f JRC 与分形维数
η )
Table 3 The typical rough crack profile and its JRC ( f JRC ) and fractal dimension (
编号 典型裂隙剖面 f JRC η 编号 典型裂隙剖面 f JRC η
1 0～2 1.002 6 10～12 1.036

2 2～4 1.005 7 12～14 1.043
3 4～6 1.011 8 14～16 1.051

4 6～8 1.018 9 16～18 1.062

5 8～10 1.025 10 18～20 1.069

取分形维数 η 分别为 1、1.05 和 1.1 等 3 种工况探讨裂隙分形维数对岩体动力学特性的影响，计算
结果如图 7 所示。可以看出，与图 6 曲线类似，当分形维数 η 由 1 分别增加到 1.05 和 1.1 时，应力-应变曲
线 的 斜 率 及 峰 值 强 度 点 均 呈 现 增 加 趋 势 ： 岩 体 动 态 峰 值 强 度 由 2 6 . 4 2 M P a 分 别 增 加 到 2 7 . 8 4 和
28.77 MPa，增加幅度分别为 5.37% 和 8.89%；弹性模量由 8.15 GPa 分别增加到 8.88 和 9.60 GPa，增加幅度
分别为 8.96% 和 17.79%。该计算结果也同样说明裂隙粗糙度对岩体动态力学特性有较大影响，且随着
分形维数 η 的增加，其影响程度也呈现出逐渐增加的趋势。需要说明的是虽然该结论与采用粗糙度系
f JRC 时得出的结论类似，但是该方法的优点是一方面拓展其应用领域，即裂隙粗糙程度的取值没有限
数
制，不像 f C 最大值只能取为 20；另一方面是对裂隙粗糙度的刻画也更为精确，提高了计算精度。
JR

061411-7