Page 27 - 《爆炸与冲击》2025年第6期

第 45 卷 单仁亮，等： 深部岩体结构面动力特性与致灾效应研究进展 第 6 期

8
k n =0 k n =2 GPa/m 8 k n =0 8 k n =0
k n =4 GPa/m
k n =1 GPa/m Cycle 4 Cycle 5 k n =1 GPa/m k n =1 GPa/m
Shear stress/MPa 4 2 Shear stress/MPa 6 4 2 k n =4 GPa/m Shear stress/MPa 6 4 2 k n =4 GPa/m
6
k n =2 GPa/m
k n =2 GPa/m
Cycle 3
Cycle 1 Cycle 2
0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25
Shear displacement/mm Shear displacement/mm Shear displacement/mm
(a) α=15° (b) α=30° (c) α=45°
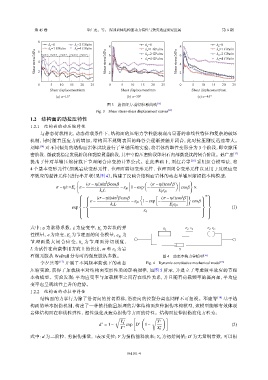
图 3 剪切应力-剪切位移曲线 [13]
Fig. 3 Shear stress-shear displacement curves [13]
1.2 结构面的动拉压特性

1.2.1 结构面的动压缩特性
与静态荷载相比，动态荷载条件下，结构面的压缩力学性能表现出显著的非线性特征和复杂的破坏
机制，同时随着压应力的增加，结构面不规则表面的峰谷会逐渐接触并闭合，此时抗压刚度迅速增大。
刘峰 [14] 对不同倾角的结构面岩体试块进行了单轴压缩实验，将岩体的塑性变形分为 3 个阶段，即空隙压
密阶段、微破裂稳定发展阶段和裂隙贯通阶段，其中空隙压密阶段即岩石内部微裂纹的闭合阶段。孙广忠 [15]
提出了针对单轴压缩荷载下节理闭合应变的计算公式。在此基础上，刘红岩等 [16] 采用组合模型法，将
4 个基本变形元件（细观岩块变形元件、节理面剪切变形元件、节理面闭合变形元件以及用于反映应变
率效应的黏性元件）进行串并联（见图 4），构建了反映含结构面岩体的动态单轴压缩损伤本构模型：
® 2 ï Å ãò ´
2
(σ−η˙ε)sin βcosβ (σ−η˙ε)cos β
σ−η˙ε =E r ε− −ε j0 1−exp − cosβ ×
k s L E j ε j0
 
 2 ß ï 2 ò™ m
 (σ−η˙ε)sin βcosβ (σ−η˙ε)cos β 
   
 ε− −ε j0 1−exp − cosβ 
   
k s L E j ε j0
exp − (1)
  ε 0  
   
   
 

式中：η 为黏滞系数， ˙ ε 为应变率，E 为岩块的弹 D a σ j , ε j1 σ j , ε j2
r
ε 为应变，E 为节理面的闭合模量，ε 为
j
0
j
性模量，
节 理 面 最 大 闭 合 应 变 ， k 为 节 理 面 剪 切 刚 度 ，
s
0
L 为试件在荷载作用方向上的长度，m 和 ε 为岩 η
石微元服从 Weibull 分布时的强度服从参数。 图 4 动态本构力学模型 [16]
李夕兵等 [17] 开展了不同频率荷载下的动态 Fig. 4 Dynamic constitutive mechanical model [16]
压缩实验，获得了加载频率对结构面变形性质的影响规律，如图 5 所示，并建立了考虑频率效应的节理
本构模型。实验发现：平均应变率与加载频率之间存在线性关系，并且随着荷载频率的提高加，平均应
变率也呈现线性上升的趋势。

1.2.2 结构面的动拉伸特性
结构面的力学行为除了沿切向的剪切滑移，沿法向的拉裂分离也同样不可忽视。邓建等 [18] 基于结
构面的基本损伤机制，构建了一种依托能量原理的岩体结构面拉伸损伤本构模型，该模型能够有效体现
岩体结构面在非线性弹性、塑性强化及疲劳损伤等方面的特性。结构面拉伸损伤演化方程为：
… + ñ Ç åô
Y Y +
+ 0 +
d = 1− exp D 1− (2)
Y + Y 0 +
+
式中：d 为二阶拉、剪损伤张量，+表示受拉；Y 为损伤能释放率；Y 为初始阀值；D 为无量纲常数，可以根
0
061101-4