Page 146 - 《爆炸与冲击》2025年第5期

第 45 卷 康普林，等： 考虑药包爆破动-静时序作用的漏斗形成机理 第 5 期

p i
p b = n (4)
(R/R 0 )
式中：p 为应力波传播距离 R 后的压力，n 为衰减指数。n 可表示为：
b
µ
n = 2± (5)
1−µ
式中：μ 为岩石的泊松比，冲击波影响范围内取正号，应力波影响范围内取负号。
假设爆生气体的膨胀过程为绝热膨胀，忽略进入岩体裂隙的爆生气体体积，炮孔壁受爆生气体压力
作用发生位移，炮孔逐渐扩张，爆腔内压力随之发生变化，其大小可根据爆生压力状态方程由爆腔体积
近似求出。爆生压力状态方程 [33] 为：
Å ã γ
V 0
p(t) = p 0 (6)
V
0
式中：p 、V 分别为炮孔的初始压力和初始体积，p(t)、V 分别为 t 时刻的爆腔压力和爆腔体积，γ 为与炸
0
药及岩石性质相关的常数。
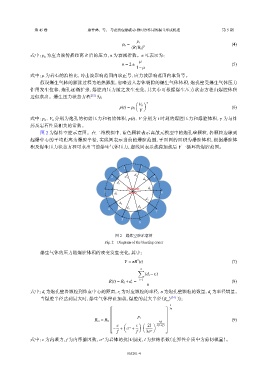
图 2 为爆炸空腔示意图。在二维模拟中，蓝色颗粒表示离散元模型中的炮孔壁颗粒，各颗粒边缘到
起爆中心的平均距离为爆腔半径，实线圆表示当前的爆腔范围，平面圆的面积为爆腔体积，根据爆腔体
积及爆生压力状态方程可求出当前爆生气体压力，虚线圆表示载荷加载后下一循环的爆腔范围。

1 i
2 d 1 d i 9
d 9
d 2
Blasting d 8
3 crater 8
d 3
d 7
d 4
4 d 5 d 6 7

5
6

图 2 爆炸空腔示意图
Fig. 2 Diagram of the blasting crater
爆生气体的压力随爆腔体积的改变发生变化，其中：

2
V = πR (t) (7)
n
∑
(d i −r i )
R(t) = R 0 +d r = i=1 (8)
n
式中：d 为炮孔壁各颗粒到炸点中心的距离，r 为对应颗粒的半径，n 为炮孔壁颗粒的数量，d 为半径增量。
i
r
i
当爆腔半径达到最大时，爆生气体停止加载，爆腔的最大半径（R ） [34] 为：
m
1
 
3γ
 
 
p i
(9)
 
R m = R 0 
4f 
Å ãÅ ã
c c 2l 3(1+f) 

− + σ +
∗
f f 3σ ∗
σ ∗ 为岩体的抗压强度，l 为拉梅系数（在弹性介质中为剪切模量）。
式中：c 为内聚力，f 为内摩擦因数，

055201-4