Page 148 - 《爆炸与冲击》2025年第5期

第 45 卷 康普林，等： 考虑药包爆破动-静时序作用的漏斗形成机理 第 5 期

3.0
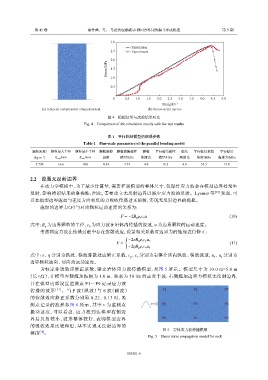
Simulation
2.5 Experiment
2.0
Stress/MPa 1.5

1.0

0.5

0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Strain/10 −3
(a) Uniaxial compression simulation test (b) Stress-strain curves
图 4 模拟结果与试验结果对比
Fig. 4 Comparison of the simulation results with the test results

表 1 平行黏结模型的细观参数
Table 1 Fine-scale parameters of the parallel bonding model

颗粒密度/ 颗粒最大半径 颗粒最小半径 颗粒摩擦 颗粒接触弹性 颗粒 平行黏结弹性 黏结 平行黏结抗拉 平行黏结
−3
(kg·m ) R max /mm R min /mm 因数 模量/GPa 刚度比 模量/GPa 刚度比 强度/MPa 黏聚力/MPa
2 730 16.6 10.0 0.54 3.79 4.0 16.2 4.0 53.5 19.8

2.2 设置无反射边界
在动力学模拟中，为了减少计算量，需要控制模型的整体尺寸，但爆炸应力波会在模型边界处发生
反射，影响模拟结果的准确性，因此，需要建立无反射边界以减少应力波的反射。Lysmer 等 [36] 发现，可
以在模型边界施加与速度方向相反的力吸收传播过来的波，实现无反射边界的模拟。
施加的边界力（F）与对应颗粒运动速度的关系为：
F = −2R p ρ r c 0 u (10)

式中：R 为边界颗粒的半径，c 为应力波在岩体内传播的波速，u 为边界颗粒的运动速度。
0
p
考虑到应力波在传播过程中存在弥散效应，设置相关系数对边界力的施加进行修正：
®
−2εR p ρ r c p u n
F = (11)
−2ηR p ρ r c s u s
式中：ε、η 分别为纵波、横波弥散效应修正系数，c 、c 分别为岩体介质内纵波、横波波速，u 、u 分别为
s
s
p n
边界颗粒法向、切向的运动速度。
为标定弥散效应修正系数，建立岩体应力波传播模型，如图 5 所示。模型尺寸为 10.0 m×5.0 m
（长×高），在模型左侧施加振幅为 1.0 m、频率为 50 Hz 的正弦半波，右侧施加边界力模拟无反射边界，

并在模型内部设置监测点 P1～P9 记录应力波
传 播 的 波 形 [37] 。 当 P 波 （ 纵 波 ） 与 S 波 （ 横 波 ） P1 P4 P7
的 弥 散 效 应 修 正 系 数 分 别 取 0.22、 0.13 时 ， 监
测 点 记 录 的 波 形 如 图 6 所 示 ， 其 中 v 为 监 测 点 P2 P5 P8
振 动 速 度 ， 可 以 看 出 ， 应 力 波 到 达 模 型 右 侧 边
界 后 反 射 较 小 ， 波 形 整 体 较 好 ， 表 明 模 型 边 界 P3 P6 P9
的吸收效果比较理想，基本实现无反射边界的
图 5 岩体应力波传播模型
模拟 [38] 。

Fig. 5 Stress wave propagation model for rock

055201-6