Page 145 - 《爆炸与冲击》2025年第5期

第 45 卷 康普林，等： 考虑药包爆破动-静时序作用的漏斗形成机理 第 5 期

作用 [22] ；随着爆炸动力学的发展，相关理论则认为岩石破碎主要是由爆炸应力波引起的 [23] ；目前，国内外
普遍认可的是爆生气体和爆炸应力波共同作用理论 [24] 。爆炸应力波与爆生气体的加载特点不同，爆炸
应力波的加载率较大，衰减较快，作用时间较短；爆生气体的加载率较小，衰减较慢，作用时间较长。因
此，为较准确地模拟爆破漏斗的形成过程，必须充分考虑爆炸应力波和爆生气体不同的加载特点。
较早的离散元爆破模拟中，爆炸载荷的施加通常不区分应力波与爆生气体，共同考虑两者，以三角波 [25]
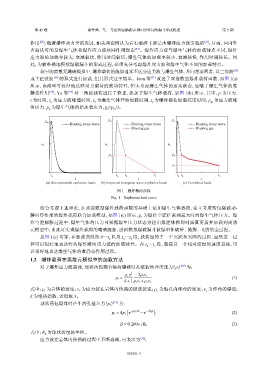
或半正弦波 [26] 的形式进行加载，但其形式过于简单。Jeon 等 [27] 改进了双指数型爆炸载荷函数，如图 1(a)
所示，该模型可较好地反映动力载荷的波动特性，但未考虑爆生气体的运动状态，忽略了爆生气体的准
静态作用 [28] ；Ye 等 [29] 对三角波载荷进行了修正，添加了爆生气体载荷，如图 1(b) 所示，其中，p 为压力，
t 为时间，t 为应力波峰值时间，t 为爆生气体开始加载时间，t 为爆炸载荷加载结束时间，p 为应力波峰
u
d
m
s
值应力，p 为爆生气体初始加载应力，p =p /3。
d
d
m

p m p m
p m
Blasting stress wave Blasting stress wave Blasting stress wave
Blasting gas Blasting gas
p p p
p d
p d
p r
t u t u t d t s t u t d t s
t t t
(a) Bi-exponential explosive loads (b) Improved triangular wave explosive loads (c) Combined loads
图 1 爆炸载荷曲线
Fig. 1 Explosion load curve

综合考虑上述理论，在双指数型爆炸载荷函数的基础上添加爆生气体载荷，建立考虑药包爆破动-
静时序作用的爆炸载荷联合加载模型，如图 1(c) 所示，p 为爆炸空腔扩张到最大时的爆生气体压力。爆
r
炸空腔膨胀过程中，爆生气体的压力可根据爆生压力状态方程由爆腔体积即时演算更新并加载到离散
元模型中，由此可实现爆炸载荷的精确施加，进而模拟爆破漏斗被爆岩体破碎、抛掷、飞散的全过程。
从图 1(c) 可知，在加载曲线的 0～t 以及 t ～t 段，载荷经历了一个突跃和突降的过程，显然这一过
d
u
u
程可以很好地表达炸药爆炸瞬间应力波的加载特性。在 t ～t 段，载荷以一个相对缓慢的速度衰减，可
s
d
以很好地表达爆生气体的准静态作用过程。

1.2 爆炸载荷在离散元模拟中的加载方法
对于爆炸应力波载荷，球状药包耦合装药爆破时孔壁初始冲击压力（p ） [30] 为：
i
ρ c v 2 2ρ r v r
p i = c (1)
k +1 ρ r v r +ρ c v c
式中：ρ 为岩体的密度；v 为应力波在岩体内传播的纵波波速；ρ 为炮孔内炸药的密度；v 为炸药的爆速；
c
r
c
r
k 为绝热指数，近似取 3。
球状药包爆炸时产生的孔壁压力（p ） [31] 为：
t
Ä √ √ ä
p t = 4p i e −βt/ 2 −e − 2βt (2)
(3)
β = 0.269v r /R 0
式中：R 为球状药包的半径。
0
应力波在岩体内传播的过程中不断衰减，可表示为 [32] ：

055201-3