Page 126 - 《爆炸与冲击》2023年第2期

第 43 卷 李嘉皓，等： 液压膨胀环恒应变率加载技术 第 2 期

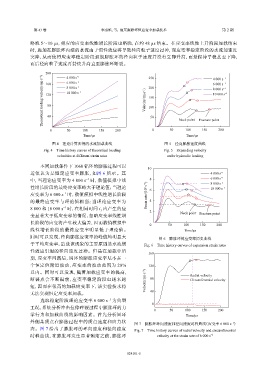
略晚 5～10 µs，相应的应变率线性增长阶段也略晚，在约 48 µs 结束。在应变率线性上升阶段加载结束
时，施加在膨胀环内壁的水流由于惯性效应将导致径向粒子速度过冲，而应变率稳定阶段的水流加速度
突降，从而使得应变率稳定阶段初期膨胀环的径向粒子速度并没有立即升高，而是保持平稳甚至下降，
而后径向粒子速度再持续升高直至膨胀环断裂。

200 4 000 s −1 250 4 000 s −1
Theoretical loading velocity/(m⋅s −1 ) 120 8 000 s −1 Velocity/(m⋅s −1 ) 200 8 000 s −1 −1
6 000 s
−1
6 000 s
160
−1
−1
10 000 s
10 000 s
150
80
100
40
150
100
0 50 100 150 200 50 0 50 Neck point Fracture point 200
Time/μs Time/μs

图 4 理论计算所得的水流加载曲线 图 5 径向膨胀速度曲线
Fig. 4 Time history curves of theoretical loading Fig. 5 Expanding velocity
velocities at different strain rates under hydraulic loading
不同加载条件下 1060 铝环的膨胀过程可以 10
近似认为是恒定应变率膨胀，如图 6 所示。其 4 000 s −1
中，当理论应变率为 4 000 s 时，数值模拟中线 8 6 000 s −1
−1
8 000 s
−1
性增长阶段的最终应变率略大于理论值；当理论 6 10 000 s −1
应变率为 6 000 s 时，数值模拟中线性增长阶段 Strain rate/(10 3 s −1 )
−1
的最终应变率与理论值相当；当理论应变率为 4
−1
1
8 000 和 10 000 s 时，在相同时间 t 内产生的应
2 Neck point Fracture point
变显著大于低应变率的情况，忽略应变率线性增
长阶段的应变将产生较大偏差，因而数值模拟中 0 50 100 150 200
线性增长阶段的最终应变率明显低于理论值。 Time/μs

同时可以发现，径向膨胀应变率的峰值均明显大 图 6 膨胀环的应变率历史曲线
于平均应变率，造成该现象的主要原因是水流惯 Fig. 6 Time history curves of expansion strain rates
性效应引起的径向速度过冲。但是在加载中后 160
期，应变率回落后，圆环的膨胀应变率基本在一
个恒定值附近波动，应变率的波动范围为 20% 120
以内。同时可以发现，随着加载应变率的提高， Radial velocity
断裂点会不断提前，应变率稳定阶段也越来越 Velocity/(m⋅s −1 ) 80 Circumferential velocity
短，因而在很高的加载应变率下，该实验技术将
无法实现恒定应变率加载。 40
选取稳定阶段理论应变率 6 000 s 为典型
−1
0
工况，系统分析冲击拉伸碎裂过程中膨胀环的力
0 50 100 150 200
学行为和加载曲线的影响因素。首先分析圆环 Time/μs

外侧某质点在膨胀过程中的质点速度和应力状
−1
图 7 膨胀环环向速度和径向速度时程曲线（应变率 6 000 s ）
态。图 7 给出了膨胀环的环向速度和径向速度 Fig. 7 Time history curves of radial velocity and circumferential
时程曲线，在膨胀环发生显著颈缩之前，膨胀环 velocity at the strain rate of 6 000 s −1

024101-5