Page 339 - 《软件学报》2020年第9期

2960 Journal of Software 软件学报 Vol.31, No.9, September 2020

加高效,同时,由于这些卷积的代码长度较短,循环展开后编译器能够更有效地进行指令调度等优化;另一方面,
cuSPARSE 和 Escoin 对小卷积的优化不足.类似 cuBLAS,他们在小卷积上的性能与大规模卷积的性能之间存在
明显差距.这使得在很低的稀疏程度下,我们生成的算子性能就可以显著超过 cuSPARSE 和 Escoin.另外,当稀疏
程度很高时(0.8~0.9),cuSPARSE 的性能相对较低稀疏程度有所改善.但我们生成的稀疏算子仍能获得 5.5~59.5
倍的加速.在所有的算子和稀疏程度下,我们的方法都能获得相对 cuSPARSE 至少 5.5 倍的加速.对于批大小为 1
的场景,在 0.1~0.9 的稀疏程度下,我们的方法对于 cuSPARSE 可以获得 1.2 倍~22.9 倍的加速.
我们的方法对 Escoin 的性能优势也很明显.在批大小为 64 和 1 时,我们的方法在所有稀疏程度和算子上平
均可实现 18.1 倍和 4.1 倍的加速.我们在代码中发现:Escoin 中存在众多硬编码的固定的优化参数(例如 tile size
等)以及 kernel 选择规则,这些参数与具体问题规模和平台相关,限制了 Escoin 在其他平台和算子上的性能表现.
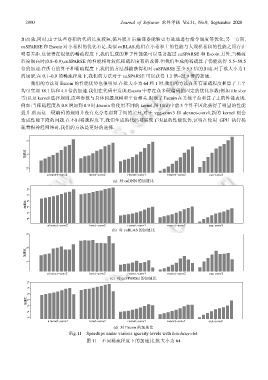
例如:当稀疏程度从 0.8 增加到 0.9 时,Escoin 将使用不同的 kernel,图 11(d)中前 3 个算子因此获得了明显的性能
提升.然而这一硬编码的规则并没有充分考虑算子间的差异,对于 vgg-conv3 和 alexnet-conv1,新的 kernel 则会
造成性能下降的问题.在不同稀疏程度下,我们生成的代码都展现了明显的性能优势,证明在使用 GPU 执行稀
疏卷积神经网络时,我们的方法是更好的选择.

(a) 对 cuDNN 的加速比

(b) 对 cuBLAS 的加速比

(c) 对 cuSPARSE 的加速比

(d) 对 Escoin 的加速比
Fig.11 Speedups under various sparsity levels with batchsize=64
图 11 不同稀疏程度下的加速比,批大小为 64