Page 335 - 《软件学报》2020年第9期

2956 Journal of Software 软件学报 Vol.31, No.9, September 2020

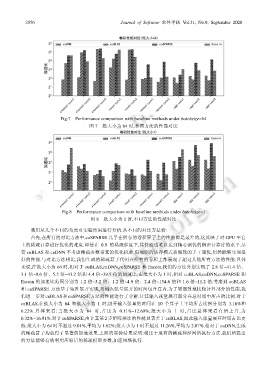
Fig.7 Performance comparison with baseline methods under batchsize=64
图 7 批大小为 64 时,不同方法的性能对比

Fig.8 Performance comparison with baseline methods under batchsize=1
图 8 批大小为 1 时,不同方法的性能对比

我们从几个不同的角度对实验结果进行分析.从不同的对比方法看:
首先,在所有的对比方法中,cuSPARSE 几乎在所有的卷积算子上的性能都是最差的,这反映了对 GPU 平台
上的稀疏计算进行优化的难度.即使在 0.9 的稀疏程度下,其性能也难以达到精心调优的稠密计算库的水平.尽
管 cuBLAS 和 cuDNN 不考虑稀疏参数带来的优化机会,但规则的访存模式和细致的手工调优,仍然能够实现很
好的性能.与对比方法相比,我们生成的稀疏算子代码在所有的卷积上都展现了超过其他所有方法的性能.具体
来说,在批大小为 64 时,相对于 cuBLAS,cuDNN,cuSPARSE 和 Escoin,我们的方法分别实现了 2.8 倍~41.4 倍、
3.1 倍~9.6 倍、5.5 倍~43.2 倍和 4.4 倍~39.5 倍的加速比;在批大小为 1 时,相对 cuBLAS,cuDNN,cuSPARSE 和
Escoin 的加速比范围分别为 1.2 倍~3.2 倍、1.2 倍~4.9 倍、2.4 倍~154.6 倍和 1.6 倍~11.2 倍.考虑到 cuBLAS
和 cuSPARSE 方法基于矩阵展开实现,将输入张量展开的时间包含在内.为了更细致地比较计算部分的性能,我
们进一步对 cuBLAS和 cuSPARSE 方法的性能进行了分解,计算输入张量展开部分在总时间中所占的比例.对于
cuBLAS,在批大小为 64 和批大小为 1 时,展开输入张量的时间在 10 个算子上平均所占比例分别为 3.16%和
6.22%.具体来看:当批大小为 64 时,占比为 0.11%~12.69%;批大小为 1 时,占比总体来看有所上升,为
0.32%~16.91%.对于 cuSPARSE,由于其第 2 步矩阵乘法的性能显著差于 cuBLAS,因此输入张量展开时间占比更
低.批大小为 64 时不超过 9.01%,平均为 1.62%;批大小为 1 时不超过 11.26%,平均为 2.07%.相对于 cuDNN,生成
的稀疏算子均获得了显著的加速效果.上面的实验结果说明:相比于现有的稀疏神经网络执行方法,我们所提出
的方法能够有效利用压缩后的稀疏模型参数,加速网络执行.