Page 332 - 《软件学报》2020年第9期

董晓 等:面向稀疏卷积神经网络的 GPU 性能优化方法 2953

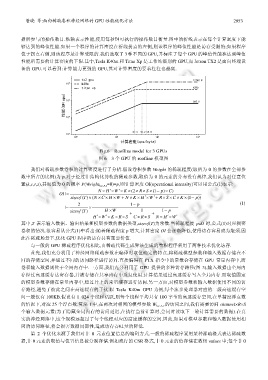
据所参与的操作数目.纵轴表示性能,使用每秒钟可执行的操作数目衡量.图中的折线表示在每个计算密度下能
够达到的峰值性能.如果一个程序的计算密度在折线拐点的左侧,则该程序的峰值性能是访存受限的;如果程序
位于拐点右侧,则该程序是计算受限的.我们选取了 3 种不同的 GPU,并标注了每个 GPU 的峰值性能和达到峰值
性能所需要的计算密度的下限.其中,Tesla K40m 和 Titan Xp 是工作站级别的 GPU,而 Jetson TX2 是面向终端设
备的 GPU.可以看到:计算能力更强的 GPU,其对计算密度的要求往往也越高.

Fig.6 Roofline model for 3 GPUs
图 6 3 个 GPU 的 roofline 模型图
我们对稀疏参数卷积的计算密度进行了分析.假设卷积参数 Weight 的稀疏程度(取值为 0 的参数在全部参
数中所占的比例)为 p.对于经过非结构化剪枝的稀疏参数,取值为 0 的元素的分布没有规律,我们认为对任意位
置(k,c,r,s),其取值为 0 的概率 P(Weight k,c,r,s =0)=p,则计算密度 OI(operational intensity)可以用公式(1)表示:
×
NH′× W′× K × (2 R S × × (1 p × − ) C )
×
OI |=
×
−
sizeof T × () (N C H W + × NKH′× × W′× + R S C K × × (1 p ))
×
×
×
2 1 p (1)
−
|= ×
−
×
sizeof T HW + 1 + 1 p
()
H′ W′× × KR S C R S NH′× W′×
××
××
其中,T 表示输入数据、输出结果和模型参数的数据类型,sizeof(T)为常数.当稀疏程度 p=0 时,公式(1)对应稠密
卷积的情况.很容易从公式(1)中看出:随着稀疏程度 p 增大,计算密度 OI 会逐渐降低,使得访存容易成为瓶颈.因
此在稀疏场景下,优化 GPU 程序的访存具有重要价值.
与一般的 GPU 稀疏程序优化相比,由稀疏代码生成算法生成的卷积程序采用了两种技术优化访存.
首先,我们充分利用了神经网络稀疏参数在编译时取值确定的特点,将稀疏模型参数和输入数据存储在不
同的存储空间,并通过不同的访问路径进行访问.直接编码在 PTX 指令中的常数会存储在 GPU 常量内存中,而
卷积输入数据则位于全局内存中.一方面,我们充分利用了 GPU 提供的多种访存路径(图 3),输入数据由全局内
存经过高速缓存达寄存器,并被存储在共享内存中反复使用.计算结果通过高速缓存写入全局内存.而取值固定
的模型参数存储在常量内存中,经过片上的常量缓存进行访问.另一方面,对模型参数和输入数据使用不同的访
存路径,避免了彼此之间在高速缓存的干扰.以 Tesla K40m GPU 为例,每个流多处理器对应的二级高速缓存空
间一般仅有 100KB.假设有 1 024 个线程活跃,则每个线程平均只有 100 字节的高速缓存空间,在单精度浮点数
的情况下,对应 25 个浮点数.算法 1 中,在两次对相同的模型参数 W k,c,r,s 的访问之间,我们需要访问 channel×R×S
个输入数据元素(为了隐藏全局内存的访问延迟,在执行当前计算时,会同时读取下一轮计算需要的数据).在真
实的神经网络中,这个规模远超过了每个线程对应的高速缓存的空间.因此,如果对模型参数和输入数据使用相
同的访问路径,将会损害数据局部性,造成访存吞吐量的降低.
第 2 个优化来源于我们对非 0 元素位置信息的编码方式.一般的稀疏程序采用某种稀疏格式表达稀疏数
据,非 0 元素的取值与位置信息被分别存储.例如流行的 CSR 格式,非 0 元素的值存储在数组 values 中;每个非 0