Page 159 - 《软件学报》2020年第9期

2780 Journal of Software 软件学报 Vol.31, No.9, September 2020

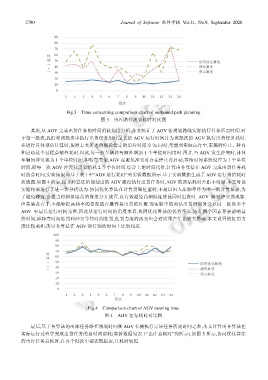
Fig.3 Time-consuming comparison chart of outbound path planning
图 3 出库路径规划耗时对比图

其次,从 AGV 完成出货任务的时间消耗角度分析,本文统计了 AGV 按规划路线实际执行任务所需时间.对
于每一批次,我们将该批次中执行出货任务用时最长的 AGV 运行时间计为该批次的 AGV 执行出货任务耗时.
在进行具体预估计算时,按照上文所述的假设给定的单位时间为 2s.同时,考虑到实际运行中,车辆的停止、转向
和启动这个过程会额外耗时.因此,每一次车辆转弯额外增加 1 个单位时间用时.再者,当 AGV 发生冲突时,计算
车辆间冲突视为 1 个单位时间,和转弯类似,AGV 在避免冲突时存在停止再启动,等待时间系统设置为 1 个单位
时间,即每一次 AGV 冲突共需要消耗 2 个单位时间.综合上述时间代价,计算出各算法在 AGV 完成出货任务耗
时的总时间,实验结果如基于表 1 中“AGV 运行耗时”列实验数据所示.基于实验数据生成了 AGV 运行预估耗时
折线图.如图 4 所示,按 3 种算法所规划出的 AGV 路径执行出货任务时,AGV 的预估耗时差距不明显.本文对该
实验结果进行了进一步分析认为:协同优化算法在计算货架位置时,不是以出入库频率作为唯一的计算依据,为
了避免碰撞,会适当将相似度高的货架分开放置,以有效避免高相似度货品同时出货时 AGV 路径冲突的现象.
但其缺点在于,不能够把高频率的货架放在最容易出货的位置.而实验中的预估出货时间时会以同一批次多个
AGV 中最长运行时间为准,因此从运行时间的角度来看,协同优化算法的优势不大.还有两个因素存会影响最
终时间,即转弯时间惩罚和冲突等待时间惩罚,惩罚力度的改变也会对结果产生比较大影响.本文设置的惩罚力
度比较柔和,所以各算法在 AGV 运行预估时间上比较相近.

Fig.4 Comparison chart of AGV running time
图 4 AGV 运行耗时对比图
最后,基于各算法的出库任务路径规划时间和 AGV 车辆执行完该任务所需时间之和,本文计算出各算法在
实际运行过程中完成出货任务的总时间消耗(实验数据见表 1“出库总耗时”列所示).如图 5 所示,协同优化算法
的出库任务总耗时,在各个批次中都表现稳定,且耗时较短.