Page 67 - 《真空与低温》2025年第3期

338 真空与低温 第 31 卷 第 3 期

式中：p 为所测量的压力；p d 为谐振式传感器的品 式中：f 为谐振子的谐振频率； τ为衰减时间，是谐
质因数对应敏感压力的下限，即对应压力的测量 振子从初始幅值减少至其 1/e 时所需的时间间隔。
下限。 根据上述模型，计算了谐振子在不同结构尺寸条件下

1.2 真空阻尼分析 的气体阻尼品质因数与压力的关系。假设传感器
5
谐振状态下，谐振环的振动速度方向及其反方 的固有阻尼品质因数为 8×10 ，计算结果如图 2 所示。
向的气体分子分别受到压缩与舒张作用效果，此时
谐振环两端的压力变化如式（3）。
 ∞ 10 6
r
 2


 p ˙x = 2mn (ν x + ˙x) f(ν x )dv x
 0.9Q max


−˙x （3）
 r ∞

 2

 p −˙x = 2mn (ν x − ˙x) f(ν x )dv x 5
 10

−˙x 品质因数
√
m mv x 2 a r =3.0 mm, b r =0.2 mm
式中： f(ν x ) = e − 2kT 为分子的运动速率符合 a r =2.5 mm, b r =0.2 mm
2π kT
10 4 a r =4.0 mm, b r =0.2 mm
ν x m k T 分别为分子数量、
麦克斯韦概率分布；n、 、 、 、 a r =3.5 mm, b r =0.2 mm
a r =5.0 mm, b r =0.2 mm
分子运动速度、分子质量、玻尔兹曼常数、热力学温 a r =4.5 mm, b r =0.2 mm
3
度。环上的压力分布差异所产生的阻尼力如式（4）。 10 0.01 0.1 1 10 100
√ √ 压力/Pa
kTm √ M m
F R = (p ˙x − p −˙x )A 8nA ˙ x = 8 2π d r a r p˙x （a）环半径对气体阻尼品质因数的影响
2π RT
（4） 1.6
式中：A 为气体阻尼面积；R 为阿伏伽德罗常数；a r
为谐振环的半径；d r 为谐振环的厚度；M m 为分子摩 1.2
尔质量。因此阻尼系数与阻尼比如方程组式（5）。
 √
√ 压力测量下限/Pa
 M m
 0.8
 c r = 8 2π d r a r p


 RT

√ （5）

 √ p
 c r M m
 ζ r = = 8 √



2mω 0 RT πb r ρω 0 0.4
式中：b r 为谐振环的高度； ω 0 ρ分别为谐振子的固
、
有角频率、分子密度。测量稀薄真空环境可以忽 2.5 3.0 3.5 4.0 4.5 5.0
环半径/mm
略气体阻尼对谐振子频率漂移的影响，此时谐振器 （b）压力测量下限与环半径的关系
的品质因数与压力的关系如式（6）。
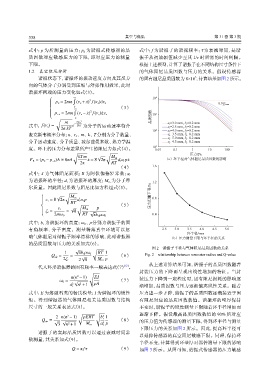
图 2 谐振子半径与气体阻尼品质因数的关系
√ √
1 πb r ρω 0 RT 1
Q air = = √ （6） Fig. 2 relationship between resonator radius and Q-value
2ζ r 2 8 M m p
从上述计算结果可知，谐振子的品质因数随着
[12]
代入环形谐振器的固有频率一般表达式（7） 。
封装压力的下降而呈现出线性增加的特征。当封
√
2
n(n −1) EI 装压力下降到一定程度时，固有阻尼损耗的影响逐
ω 0 = √ （7）
2
a 2 n +1 ρA 渐增加，品质因数与压力逐渐偏离线性关系。随着
r
式中：E 为熔融石英的杨氏模量；I 为谐振环的惯性 压力进一步下降，谐振子的品质因数逐渐接近于固
矩。得到谐振器的气体阻尼相关品质因数与结构 有阻尼对应的品质因数数值。谐振环的壁厚保持
尺寸的一般关系表达式（8）。 不变时，谐振子的线性测量下限随着环半径增加而
√
√ 逐渐下降。假设最高品质因数数值的 90% 所对应
2
2 n(n −1) ρERT b 1
5
Q air = √ √ r 5 （8） 的压力值为传感器的测量下限，得到环半径与测量
2
3 n +1 M m a p
r
下限压力的关系如图 2 所示。因此，提高环半径可
谐振子的实际品质因数可以通过衰减时间常
以延伸传感器的真空阻尼敏感下限。同理，保持环
数测量，其关系如式（9）。
半径不变，计算得到环壁厚对器件测量下限的影响
Q = πfτ （9） 如图 3 所示。从图可知，谐振式传感器的压力敏感