Page 422 - 《软件学报》2026年第1期

曹金政 等: 格上困难问题量子求解算法综述 419

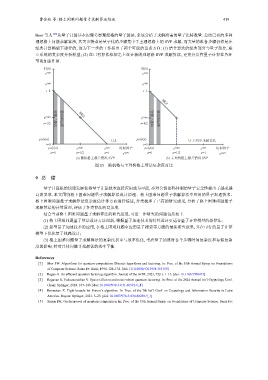
Boer 等人 [68] 从量子计算基本原理考察理想格的量子算法, 系统分析了求解所需的量子比特数量. 总结已有的多种
理想格上问题求解算法, 其突出特点是量子化的步骤集中于主理想格上的 SVP 求解, 而大量的准备步骤仍然是在
经典计算模型下进行的, 这为下一步的工作指出了两个可能的重点方向: (1) 结合算法的经典部分与量子部分, 建
立系统的复杂度分析模型; (2) 在已有算法框架之上设计新的理想格 SVP 求解算法, 更充分发挥量子计算在各环
节的加速作用.

时间 时间
e O(n t ) e O(n t )

e O(n) e O(n)
t=1 t=1 BKZ

加密、签名 全同态加密 加密、签名 全同态加密
√
√
e O ( ￣ n ) BKZ e O ( ￣ n )
t=1/2 t=1/2

poly(n) poly(n)
LLL 量子 SVP 求解算法
t=0 t=0
poly(n) e O ( ￣ n ) e O(n) 近似因子 poly(n) e O ( ￣ n ) e O(n) 近似因子
√
√
a=0 a=1/2 a=1 e O (n a ) a=0 a=1/2 a=1 e O(n a )
(a) 随机格上最差情况 SVP (b) 主理想格上最差情况 SVP
图 15 随机格与主理想格上算法复杂度对比

9 总 结

量子计算机的快速发展使得量子计算技术直接应用成为可能, 亦对公钥密码体制的量子安全性提出了越来越
高的要求. 本文围绕格上困难问题量子求解算法设计原理、格上困难问题量子求解算法中应用的量子加速技术、
格上困难问题量子求解算法复杂度估计等方面进行综述, 分类梳理了已有的研究成果, 分析了格上困难问题量子
求解算法的计算原理, 评估了各类算法的复杂度.
结合当前格上困难问题量子求解算法的研究进展, 可进一步研究的问题包括如下.
(1) 格上困难问题量子算法设计方法创新, 根据量子加速技术的特性设计更适合量子计算模型的新算法;
(2) 新型量子加速技术的应用, 在格上困难问题中应用量子搜索等方面的最新研究成果, 并在可行的量子计算
模型下优化量子线路设计;
(3) 格上困难问题量子求解算法的复杂度折中与效率优化, 考虑量子加速对各个步骤时间复杂度和存储复杂
度的影响, 针对具体问题寻找最优的效率平衡.

References
[1] Shor PW. Algorithms for quantum computation: Discrete logarithms and factoring. In: Proc. of the 35th Annual Symp. on Foundations
of Computer Science. Santa Fe: IEEE, 1994. 124–134. [doi: 10.1109/SFCS.1994.365700]
[2] Regev O. An efficient quantum factoring algorithm. Journal of the ACM, 2023, 72(1): 1–13. [doi: 10.1145/3708471]
[3] Ragavan S, Vaikuntanathan V. Space-efficient and noise-robust quantum factoring. In: Proc. of the 2024 Annual Int’l Cryptology Conf.
Cham: Springer, 2024. 107–140. [doi: 10.1007/978-3-031-68391-6_4]
[4] Bonnetain X. Tight bounds for Simon’s algorithm. In: Proc. of the 7th Int’l Conf. on Cryptology and Information Security in Latin
America. Bogotá: Springer, 2021. 3–23. [doi: 10.1007/978-3-030-88238-9_1]
[5] Simon DR. On the power of quantum computation. In: Proc. of the 35th Annual Symp. on Foundations of Computer Science. Santa Fe: