Page 361 - 《软件学报》2025年第12期

5742 软件学报 2025 年第 36 卷第 12 期

动态偏移的 动态关注的
局部图学习 全局图学习
F ˜ (1) 注意力驱动
的互补融合
动态偏移的 动态关注的
˜
局部图学习 全局图学习 F X H X
N SVD
X={x i } i=1 F ˜ (2) C
...
注意力驱动 M
的互补融合
动态偏移的 动态关注的 ˜ ×L′
局部图学习 全局图学习 F Y H Y
M F ˜ (L)
Y={y j } j=1
图 1 局部-全局动态图学习与互补融合网络 (LGCNet) 的整体框架

多层感知器
多 动 A i ˆ
f ik 态 图 f i
层 ′ f ik
感 偏 卷
f i 移 积
知
器 机 层
制
局部邻域
中心点特征 f ik λ ik x ik f ik
′ f ik
邻居点特征 x i φ(f ik −f i )
代理点特征
f i
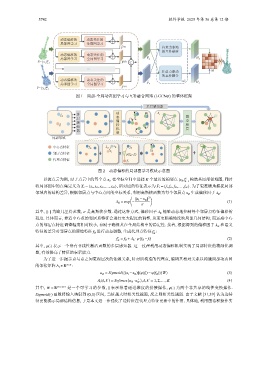
图 2 动态偏移的局部图学习模块示意图

K 构造其局部邻域图, 同时
以源点云为例, 对于点云中的每个点 x i , 在坐标空间中选择 K 个最近的相邻点 {x ik } k=1
F i = {f i ,f i1 ,f i2 ,...,f iK }. 为了更准确地捕捉局部
将局部图中的点集定义为 X i = {x i ,x i1 ,x i2 ,...,x iK }, 所对应的特征表示为
邻域内的结构差异, 根据邻居点与中心点间的坐标关系, 利用高斯核函数为每个邻居点 x ik 生成偏移因子 λ ik :

( 2 )
∥x i −x ik ∥
λ ik = exp − (1)
σ
其中, ||·|| 为欧几里得范数, σ 是高斯核参数. 通过这种方式, 偏移因子 λ ik 能够动态地控制每个邻居点特征偏移的
程度. 具体而言, 靠近中心点的邻居点特征会进行更大程度的调整, 从而更精确地反映局部几何结构; 而远离中心
点的邻居点特征调整幅度相对较小, 有助于确保其在全局结构中的稳定性. 接着, 根据得到的偏移因子 λ ik 和语义
′
f
特征的差异对邻居点的原始特征 f ik 进行动态调整, 生成代理点特征 :

ik
f = f ik +λ ik ·φ(f ik −f i ) (2)
′
ik
其中, φ(·) 表示一个带有非线性激活函数的多层感知器. 这一过程利用动态偏移机制实现了局部特征的精细化调
整, 有效提高了特征的表示能力.
为了进一步揭示点与点之间更深层次的依赖关系, 针对所构造的代理点, 编码其相对关系以构建局部动态图
的邻接矩阵 A i ∈ R K×K :

a ik = Sigmoid(((x i −x ik )||(φ(f i )−φ(f ik )))W) (3)

( )
′
A i (k,k ) = Softmax a ik ·a ′ ,k,k = 1,2,...,K (4)
⊤
′
ik
其中, W ∈ R (3+C)×1 是一个可学习的参数, || 表示沿着通道维度的拼接操作, φ(·) 为两个非共享的线性变换操作.
Sigmoid(·) 函数将输入映射到 (0,1) 区间, 当值越大时相关性越强, 反之则相关性越弱. 由于文献 [31,39] 认为边特
征更能揭示局部结构信息, 于是本文进一步强化了边特征在代理点特征更新中的作用. 具体地, 利用图卷积操作实